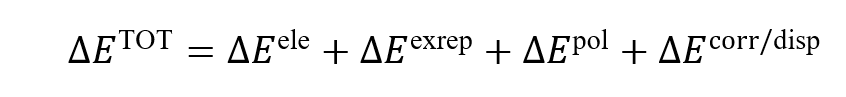Intermolecular interactions are one of the key issues in modern molecular science research. Accurate analysis of these interactions is crucial for understanding a variety of physical and chemical processes. Energy decompositionanalysis (EDA) is a quantitative analytical method based on quantum chemical calculations, which serves as a bridge between theoretical computations and conceptual explanations of molecular interactions. It plays a significant role in enhancing our understanding of various chemical phenomena.

With the rapid development of disciplines such as chemistry, materials science, and life sciences, there is an urgent need for precise and deep understanding and effective regulation of multiscale complex molecular systems, presenting new challenges to the EDA method. Recently, the Su research group combined the QM/MM method with GKS-EDA to introduce GKS-EDA(QM/MM), which is used for interactions in large molecular systems. Their work was published in J. Phys. Chem. A. 

Definitions of energy terms and Calculation Procedure

Similar to GKS-EDA, GKS-EDA(QM/MM) also decomposes interactions into terms such as electrostatic, exchange repulsion, polarization, and correlation/dispersion:

Unlike other QM/MM EDA methods, GKS-EDA(QM/MM) is compatible with various QM/MM platforms and different force fields, allowing for flexible consideration of the effects of various solvent effects on interactions. When the MM component is absent, GKS-EDA(QM/MM) should revert to the GKS-EDA results. 

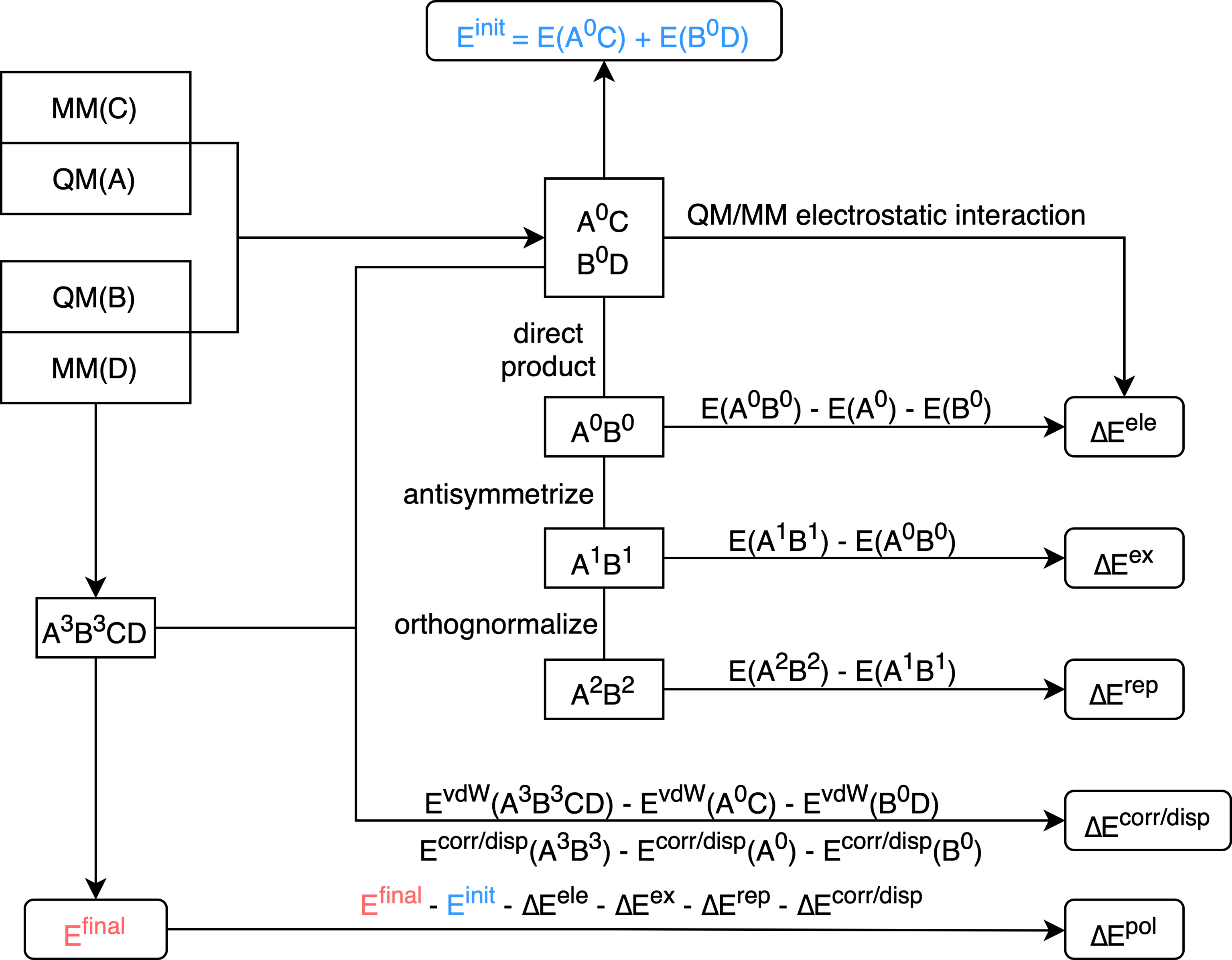
Figure 1 Calculation procedure of GKS-EDA(QM/MM)

The calculation procedure is illustrated in Figure 1. Without loss of generality, the entire system is divided into two monomers, each containing both QM and MM regions. The interactions between A and B can be directly calculated by GKS-EDA, with their initial wave functions being polarized by the MM environment of the corresponding monomers. The interactions between QM/MM and between the MM regions of the two monomers primarily include electrostatic and dispersion terms. Since they do not explicitly involve electrons, there are no exchange and repulsion interactions between the MM parts of the two monomers. Summing all electrostatic terms yields the total electrostatic interaction energy, and correlation and all dispersion terms are combined into the correlation/dispersion term. Considering that the polarization term is closely related to various force fields and the system division involves many-body effects, the polarization term is not obtained by summing each term but is derived by subtracting other terms from the total interaction energy.

GKS-EDA(QM/MM) used for solute-solvent (H3O+···water) interaction analysis

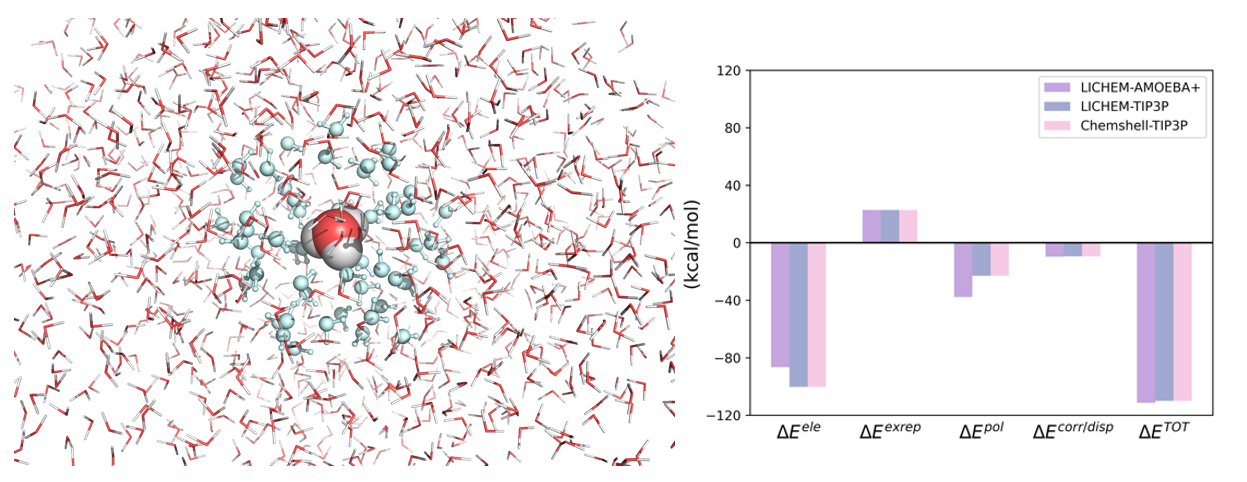
Figure 2 Solute-solvent (H₃O⁺···water) interaction

Figure 2 displays the results of GKS-EDA(QM/MM) calculations for the interactions between H3O+ and 1435 water molecules. H3O+ and the 52 water molecules in its immediate solvation layer are described using QM, while the remaining water molecules are modeled with force fields. In the QM region, H3O+ is treated as one monomer, and the first solvation layer of 52 water molecules as another monomer. As shown in the right figure, due to the maturity of the water force fields, the total interaction energies calculated with different QM/MM programs and polarized/non-polarized force fields are similar. However, polarized force fields yield a larger polarization interaction term, while non-polarized force fields tend to underestimate polarization effects. Therefore, GKS-EDA(QM/MM) can be used for evaluating and comparing various MM force fields.

GKS-EDA(QM/MM) used for protein-ligand (MMP13-pyrimidinetrione) interaction analysis

Figure 3 Protein-ligand (MMP13-pyrimidinetrione) interaction

GKS-EDA(QM/MM) can also analyze protein-ligand interactions involving Zn2+ metalloenzyme active sites. Figure 3 shows the protein-ligand interactions, with the QM portion enclosed by dashed lines. According to the GKS-EDA(QM/MM) results, there is no dominant energy term contribution in this system. Electrostatic, polarization, and correlation/dispersion all play significant roles in facilitating the binding of the protein and ligand. Hydrogen bonding and interactions between Zn2+ and the N-containing ligand determine the electrostatic and polarization terms (Zn2+ is highly polarized by the N-containing ligand). The correlation/dispersion term arises from multiple van der Waals interactions between the hydrophobic rings and carbon chains of the inhibitor and nearby protein residues, as well as the electronic correlation contributions between the QM protein residues and the ligand.

In summary, this method can be combined with different QM/MM programs to analyze interactions in complex systems such as solute-solvent, protein-ligand, and protein-protein, providing a useful tool for quantitatively understanding the patterns of molecular interactions in complex environments.

Paper:

QM/MM-Based Energy Decomposition Analysis Method for Large Systems

Xuewei Xiong, Ran Friedman*, Wei Wu, and Peifeng Su*

DOI：10.1021/acs.jpca.4c00183