Density functional theory (DFT) methods are by far the most popular approaches for electronic structure calculations. However, the "best" functional remains elusive despite the increasing variety of functionals and continuous efforts to improve their computational accuracy.  In our work published in Advanced Science, we show that the ensembles of the existing functionals are by construction more accurate than any individual functional. 

Among possible ways to construct an ensemble, we adopted one of the simplest ones based on the principle of Occam's razor: we make a weighted average of the predictions by each density functional: 

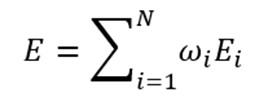
The weights are obtained via the regularized linear regression. This approach has several important benefits such as simple implementation, analytical and fast evaluation of the optimal weights, good transferability as only very few weights are optimized essentially preventing overfitting, easy evaluation of the energy derivatives and size-consistency (to the extend the individual functionals are size consistent).

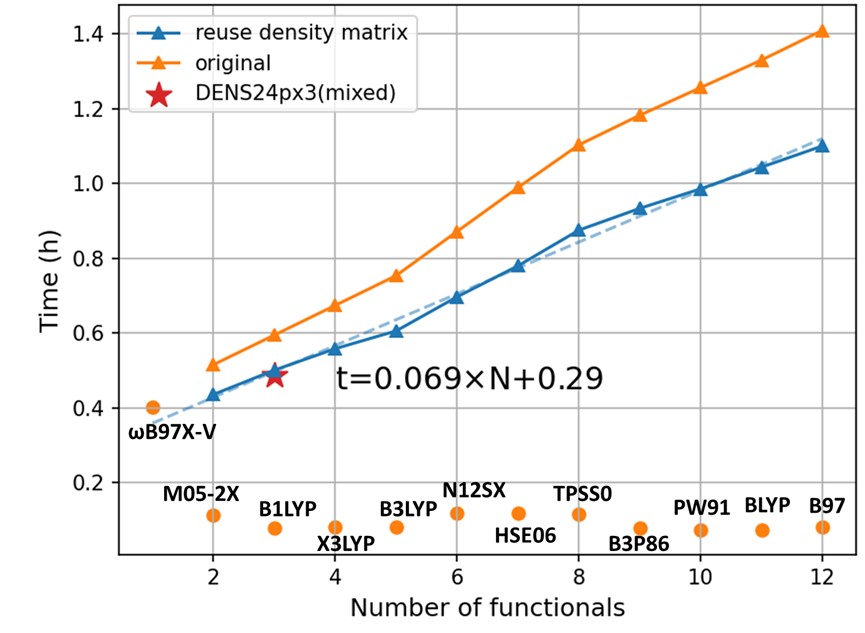
Of course, the price to pay is the increased computational cost of the ensembles but, luckily, the speed of ensembles is not that much more than the best and slow functional in the ensemble.  Also, we introduced several practical solutions for speeding up the evaluations with ensembles: we can reuse the density matrix as an initial guess for the next functional’s SCF or we can construct the mixed exchange-correlation functionals and only perform a single SCF cycle (inspired by J. Phys. Chem. A 2023, 127, 10481).

Importantly, the ensembles produce very stable predictions of electron densities, potentially ensuring the robustness of the approach for predicting other electronic structure properties. 

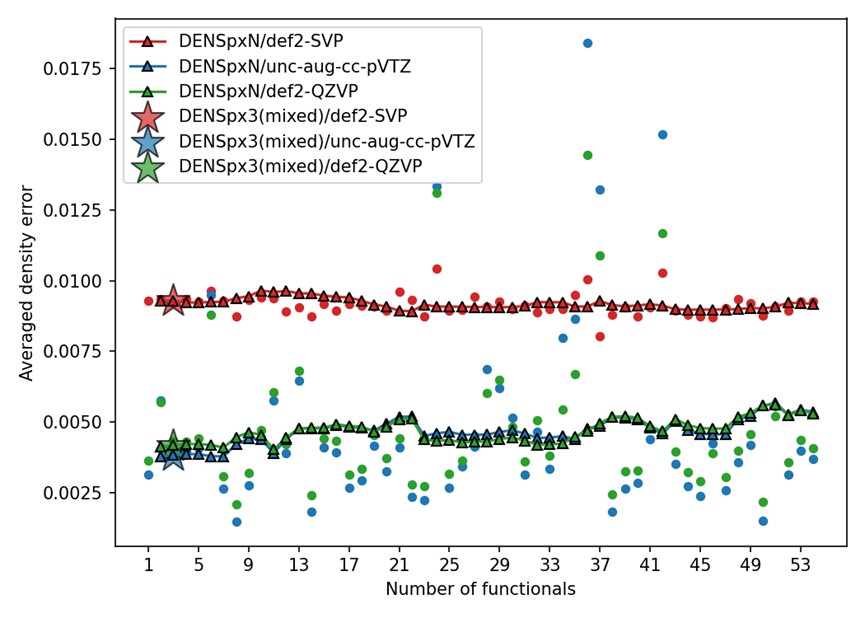
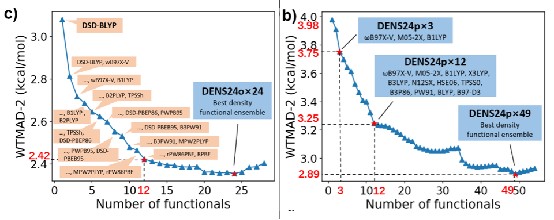
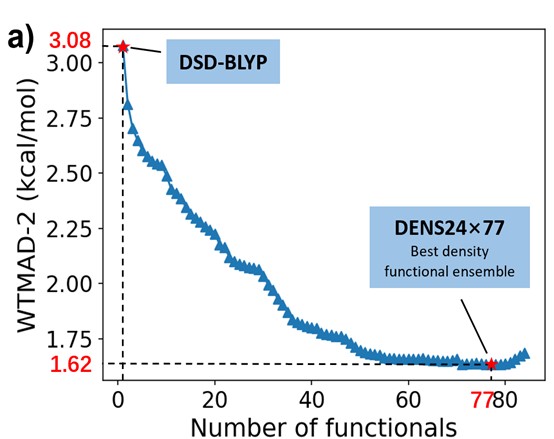
We constructed several series of the ensembles which we call DENS24, based on Orca and PySCF interfaces.  In the series, e.g., based on the PySCF interface, the number of functionals is indicated as DENS24p×N and you can select the better (and more costly) ensemble by increasing the size of the ensemble (N), similarly to increasing the size of the basis set.