Recently, the group lead by Ass. Prof. Chen in Xiamen University combines the valence bond (VB) block diabatization approach (VBBDA) with the breathing orbital VB (BOVB) theory for the study of classical but challenging covalent-ionic interaction in LiF. These methods were implemented in the versatile ab initio VB software package XMVB, and all VB computations were performed by using this program. LiF molecule has been widely studied both theoretically and experimentally as the simplest but typical molecule exhibiting the harpooning effect, in which electron transfer can occur at long distances resulting in the large crossing section of the reactions. The study shows that with highly compact wave functions, the BOVB method can be applied to investigate several atomic and molecular properties including the electron affinity of F, the adiabatic and diabatic potential energy surfaces of the two lowest-lying ¹Σ⁺ states and their energy differences at the dissociation limit, ΔE_∞, the dipole moment curve, the electronic coupling curve, the crossing distance (R_c) for LiF. The VB computation results are quite accurate as compared with the state-of-the-art molecular orbital methods, including the complete active space self-consistent field (CASSCF) and the more sophisticated complete active space second order perturbation theory (CASPT2) method, where the CASSCF method uses a rather large active space containing as many as twenty-two orbitals. This work was published in J. Chem. Phys. 2022, 157: 084106.

Figure 1. The covalent and ionic VBSCF (a, b), L-BOVB (c, d) and SL-BOVB (e, f) structures.

Firstly, the paper proposed a general VB configuration selection scheme that is specifically developed for electron transfer study. In general, the selection scheme can be regarded as the VB extension of the restricted active space self-consistent field (RASSCF) method, because it uses actually only an excitation operator in the selection process. The BOVB wave functions are extremely compact. For the largest active space of distributing six electrons on twenty-two orbitals, the number of involved covalent and ionic structures are only thirty-three and fifty-one, respectively. Meanwhile, the CASSCF wave function that exploits the same numbers of electrons and orbitals has several millions of CSFs, and the subsequent CASPT2 further involves billions of excited CSFs that can be generated from all single and double excitations of the fundamental CASSCF ones. However, with eighty-four VB structures only, covalent and ionic ones together, SA-SL-BOVB predicts good ΔE_∞ values at the CBS limit. Therefore, this selection of electronic configurations can counterbalance the electronic correlation energies in F⁻ and F.

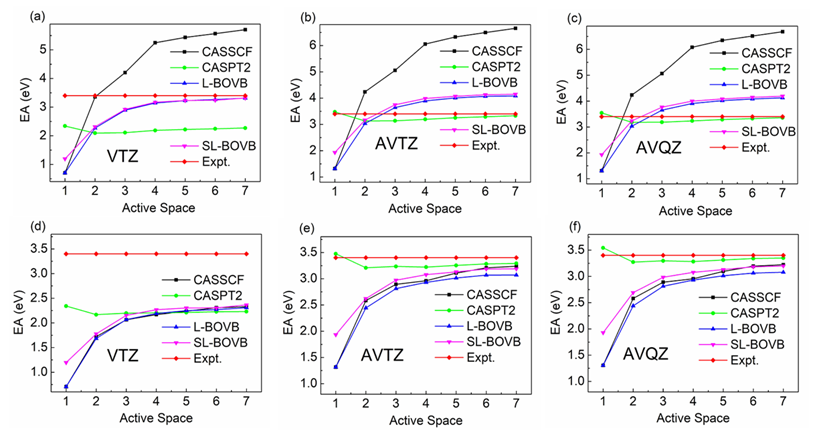
Figure 2. EA (F) calculated by various methods with different active spaces. The atom is treated at the Hartree-Fock level for (a), (b) and (c), but at the same level of active spaces as the anion for (d), (e) and (f).

Moreover, this is the first time that the BOVB results are extrapolated to the CBS limit with Dunning’s correlation consistent AVXZ basis sets. Meanwhile, the use of BOVB is also a consequence of the simultaneous correlation of the covalent and ionic states at the same level of active space. Even though the numbers of covalent and ionic structures are not the same, this might be what it should be in treating the different correlation effects in these two states because the ionic structure has one more clouded pair of electrons that needs to be correlated than the covalent one.

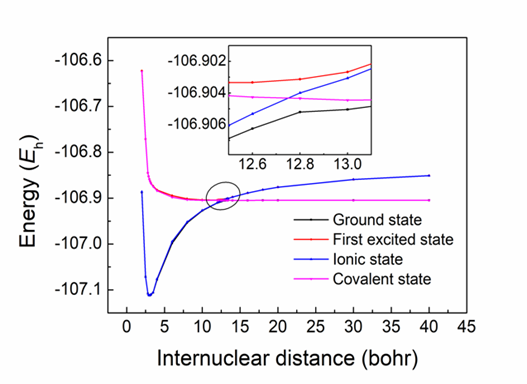
Figure 3. The PESs for the two lowest ¹Σ⁺ adiabatic and diabatic states at the SD-BOVB//CBS level.

In conclusion, with the chemical intuition from VB theory, the classic but challenging covalent-ionic interaction in the title molecule is not only conceptually interpreted but is also accurately computed. This work is mainly accomplished by graduated students Mingxing Ren (2018 PhD) and Xin Liu (2015 master). Graduated students Xuhui Lin (2016 PhD) and Lina Zhang (2017 master) participated in this work.