3. Menshutkin Reaction NH3 + CH3Cl \(\rightarrow\) [NH3CH3]+ + Cl-
3.1. Chemical question to be addressed
The last exercise is the Menshutkin reaction NH3 + CH3Cl \(\rightarrow\) [NH3CH3]+ + Cl-. The reaction is exothermic in solution. In this example, the reaction barrier in gas phase will be calculated with L-VBSCF and L-BOVB. For more information of the reaction and the computations in solution, please refer to:
3.2. Active/inactive electrons and orbitals
The reaction involves the breaking of the CH3-Cl bond and building of an NH3-CH3 bond. As such, the lone pair on NH3 and the CH3-Cl bond in the reactants constitute the active space, which involves 4 electrons on 3 orbitals. The remaining 32 electrons and 16 orbitals constitute the inactive space, including the core orbitals of N, C and Cl, 3 N-H bonds, 3 C-H bonds, and 3 s, 3 px and 3 py orbitals on Cl.
3.3. Fragmentation and important VB structures
The reaction involves 3 fragments: NH3, CH3 and Cl. The reactants include non-interacting NH3 and CH3Cl moieties while the product includes non-interacting [NH3CH3]+ and Cl- moieties. Following figure shows the important VB structures in reactant (a) and product (b).
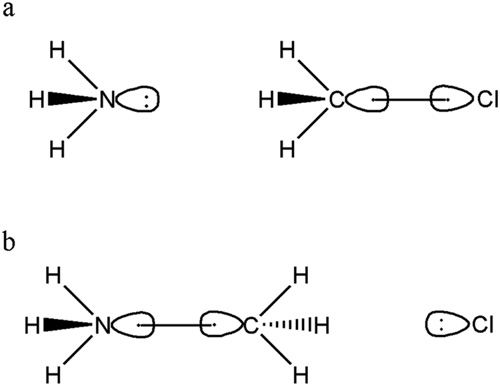
Lewis structure for the reactant (a) and product (b).
3.4. Basis set and its subsets based on orbital symmetry
6–31G* is the basis set used in this example. The basis functions are simply separated into subsets according to the atoms. The basis functions on each atom will be treated as a subset and the VB orbitals will be built with these subsets.
3.5. Structures
There are 6 VB structures involved in the active space as shown in the figure. Structures S1-S3 describe the reactant, and S3-S5 describe the product. S6 describes the electron transfer between NH3 and Cl, and will appear in the TS region.
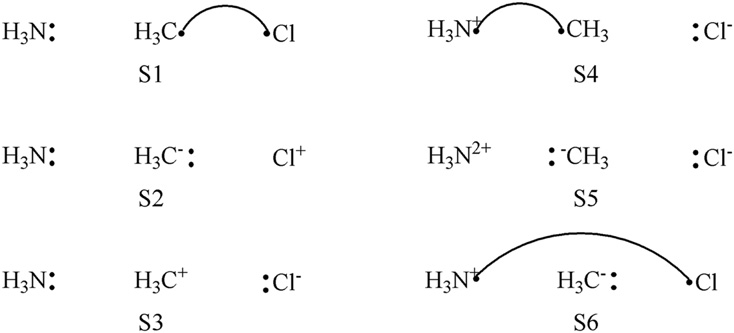
6 VB structures for Menshutkin Reaction.
3.6. Input File
The input files of L-VBSCF for reactant and TS are given below:
Reactant:
NH3CH3cl reactant
$ctrl
vbscf
nmul=1 nstr=6 iscf=5 nao=3 nae=4
orbtyp=hao frgtyp=atom
int=libcint basis=6-31G*
guess=read
$end
$stru
1:16 17 17 18 19
1:16 17 17 18 18
1:16 17 17 19 19
1:16 18 18 17 19
1:16 19 19 17 18
1:16 18 18 19 19
$end
$orb
1*5 4 4 1*3 4*3 4*3 4 4 1
6
6
6
6
6
1 7 8 9
2 3 4 5
6
6
6
1 7 8 9
1 7 8 9
1 7 8 9
2 3 4 5
2 3 4 5
2 3 4 5
1 7 8 9
2 3 4 5
6
$end
$geo
N 0.000000 0.000000 0.000000
C 0.000000 0.000000 10.000000
H -1.029985 0.000000 9.647297
H 0.514992 0.891993 9.647297
H 0.514992 -0.891993 9.647297
Cl 0.000000 0.000000 11.778400
H 0.939678 0.000000 -0.389227
H -0.469839 0.813785 -0.389227
H -0.469839 -0.813785 -0.389227
$end
TS:
NH3CH3cl
$ctrl
vbscf
nmul=1 nstr=6 nao=3 nae=4 iscf=5 itmax=300
guess=read orbtyp=hao frgtyp=atom
int=libcint basis=6-31G*
$end
$stru
1:16 17 17 18 19
1:16 17 17 18 18
1:16 17 17 19 19
1:16 18 18 17 19
1:16 19 19 17 18
1:16 18 18 19 19
$end
$orb
1*5 4 4 1*3 4*3 4*3 4 4 1
6
6
6
6
6
1 7 8 9
2 3 4 5
6
6
6
1 7 8 9
1 7 8 9
1 7 8 9
2 3 4 5
2 3 4 5
2 3 4 5
1 7 8 9
2 3 4 5
6
$end
$geo
N 0.0000000000 0.0000000000 -2.4403680000
C 0.0000000000 0.0000000000 -0.6327610000
H 1.0651490000 0.0000000000 -0.4753840000
H -0.5325745000 -0.9224460928 -0.4753840000
H -0.5325745000 0.9224460928 -0.4753840000
CL 0.0000000000 0.0000000000 1.8067450000
H -0.9550790000 0.0000000000 -2.8031240000
H 0.4775395000 0.8271226766 -2.8031240000
H 0.4775395000 -0.8271226766 -2.8031240000
$end
The input files are almost the same except the initial guess and geometry. The initial guess of reactant is given here. The initial guess of TS can be obtained from the computational results of reactant. For L-BOVB computations, the user may simply change ISCF=5 to ISCF=2 and append BOVB in $CTRL section. The initial guess of L-BOVB computations are from the computational results of correpsonding L-VBSCF computation.
3.7. Computational Results
3.7.1. The VB structures
Following table shows the VB structures involved in the calculation. The first 16 doubly occupied orbitals are inactive ones, orbital 17 corresponds to the lone pair on NH3, and orbitals 18 and 19 are singly occupied orbitals on CH3 and Cl respectively. The correspondence to the structures is also listed.
VB structure |
Structure |
|---|---|
1 ***** 1:16 17 17 18 19 |
S1 |
2 ***** 1:16 17 17 18 18 |
S2 |
3 ***** 1:16 17 17 19 19 |
S3 |
4 ***** 1:16 18 18 17 19 |
S6 |
5 ***** 1:16 19 19 17 18 |
S4 |
6 ***** 1:16 18 18 19 19 |
S5 |
3.7.2. Energies
Following table shows the total energies (in a.u.) and reaction barrier at the L-VBSCF and L-BOVB levels. Compared with the reference value 33.0 kcal mol -1 (138.1 kJ mol -1) by Webb and Gordon, L-VBSCF overestimates the reaction barrier due to the lack of dynamic correlation, and L-BOVB significantly improves the result. Compared with the energies obtained by L-VBSCF and L-BOVB, L-BOVB decreases the energy at the TS geometry much more than in the reactants. The results show that dynamic correlation plays an important role in reaction barrier calculations.
L-VBSCF |
L-BOVB |
|
|---|---|---|
\(E^{react}_{tot}\) |
-555.27775 |
-555.29156 |
\(E^{TS}_{tot}\) |
-555.21152 |
-555.24558 |
\(\Delta E^\neq\) |
41.6 |
28.8 |
3.7.3. VB wavefunction and weights
Table shows the weights of VB structures in the reactant and TS geometries. It is clear that the most important contribution comes from S1 in the reactant geometry and S3 in the TS geometry. In the TS, S4 represents the “covalent” structure of product and S3 represents the major “ionic” structure in both reactant and product. Thus, S3 represents the “bond breaking” of C-Cl and S4 shows the “bond forming” of N-C. Similar to the previous examples, L-BOVB provides larger weights for the secondary ionic structures as compared with L-VBSCF weights, which indicates that dynamic correlation plays a more important role for ionic structures than covalent ones, as already explained.
Reactant |
TS |
|||
|---|---|---|---|---|
L-VBSCF |
L-BOVB |
L-VBSCF |
L-BOVB |
|
S1 |
0.663 |
0.621 |
0.091 |
0.178 |
S2 |
0.105 |
0.120 |
-0.001 |
0.002 |
S3 |
0.232 |
0.259 |
0.532 |
0.487 |
S4 |
0.000 |
0.000 |
0.364 |
0.286 |
S5 |
0.000 |
0.000 |
-0.004 |
0.010 |
S6 |
0.000 |
0.000 |
0.017 |
0.037 |