AIQM1
New: AIQM2 is available, it has higher accuracy for barriers than AIQM1. We also highly recommend you to check out UAIQM that is our ultimate solution to the universal ML models and considered as successor to AIQM1. The only advantages of AIQM1 at the moment are: support of excited states and calibrated, accurate heats of formation, and possibility to install locally. On the XACS cloud AIQM1 has many numerical problems due to unavailability of the analytical derivatives on the cloud version.
AIQM1(人工智能-量子力学方法1)是一种通用方法,对于基态闭壳层物种,其计算精度接近于黄金标准的耦合簇量子力学方法,同时计算速度很快,与低水平半经验量子力学方法相近。此外,AIQM1也适用于带电物种、自由基物种以及激发态的计算。详情请参阅 AIQM1论文 。请将本文与其他必要的 引文 一起引用:
Peikun Zheng, Roman Zubatyuk, Wei Wu, Olexandr Isayev, Pavlo O. Dral. Artificial Intelligence-Enhanced Quantum Chemical Method with Broad Applicability. Nat. Commun. 2021, 12, 7022, DOI: 10.1038/s41467-021-27340-2.
优势: 对于闭壳层分子,AIQM1可用于精确、快速的能量计算和几何优化。
限制: 此方法目前仅可用于计算包含H, C, N, O元素的化合物。
下面我们将提供有关AIQM1安装的重要说明,以及通过命令行/输入文件和Python API来使用AIQM1的简单示例:
安装
请参阅MLatom 安装说明 。AIQM1需要 TorchANI 和 dftd4 以及半经验程序。半经验程序可以是 MNDO ,支持解析梯度和激发态计算。在 MLatom@XACS云计算平台 上无法使用MNDO,但可以使用 SCINE Sparrow 的 开发版本 (详见关于Sparrow的 论文 )。该版本不支持分析梯度,也没有AIQM1的激发态计算。因此,Sparrow可以与数值梯度一起用于几何优化和MD,但可能会导致频率计算等数值不稳定。下面描述的一些特性可能需要使用与 Gaussian 或 ASE 或PySCF包的接口。下面给出了安装说明、使用手册和适当的 引用 。
单点能计算
计算基态闭壳层分子的单点能(如果需要的话还有能量梯度)是一项简单的工作,在MLatom的输入文件中只需要3-4行,例如 sp.inp :
AIQM1 # or AIQM1@DFT or AIQM1@DFT* if you want to use these methods
xyzfile=sp.xyz
yestfile=enest.dat
ygradxyzestfile=gradest.dat
输入需要提供分子的XYZ坐标文件 sp.xyz (可以同时提供多个分子),例如含有氢气和甲烷的XYZ坐标文件 sp.xyz 如下所示(单位是Å):
2
H 0.000000 0.000000 0.363008
H 0.000000 0.000000 -0.363008
5
C 0.000000 0.000000 0.000000
H 0.627580 0.627580 0.627580
H -0.627580 -0.627580 0.627580
H 0.627580 -0.627580 -0.627580
H -0.627580 0.627580 -0.627580
当准备好输入文件 sp.inp 和 sp.xyz 以后即可运行MLatom:
mlatom sp.inp > sp.out
计算完成以后,MLatom的输出 sp.out 中会包含神经网络预测的标准差和AIQM1能量的分量:
Standard deviation of NN contribution : 0.00892407 Hartree 5.59994 kcal/mol
NN contribution : -0.00210898 Hartree
Sum of atomic self energies : -0.08587317 Hartree
ODM2* contribution : -1.09094119 Hartree
D4 contribution : -0.00000889 Hartree
Total energy : -1.17893224 Hartree
Standard deviation of NN contribution : 0.00025608 Hartree 0.16069 kcal/mol
NN contribution : 0.00958812 Hartree
Sum of atomic self energies : -33.60470494 Hartree
ODM2* contribution : -6.86968756 Hartree
D4 contribution : -0.00010193 Hartree
Total energy : -40.46490632 Hartree
用户也可以获取包含AIQM1能量的文件 enest.dat (单位是Hartree):
-1.178932238420
-40.464906315250
以及包含梯度的文件 gradest.dat (单位是Hartree/Å):
2
0.000000000000 0.000000000000 0.000032023551
0.000000000000 0.000000000000 -0.000032023551
5
-0.000000000000 -0.000000000000 0.000000000000
0.000490470799 0.000490470714 0.000490470881
-0.000490470799 -0.000490470714 0.000490470881
0.000490470799 -0.000490470714 -0.000490470881
-0.000490470799 0.000490470714 -0.000490470881
用户也可以在Python API中进行相同的计算。代码如下:
import mlatom as ml
# read molecule from .xyz file
molDB = ml.data.molecular_database.from_xyz_file('sp.xyz')
# define method
model = ml.models.methods(method='AIQM1', qm_program='MNDO')
# perform the calculations
model.predict(molecular_database=molDB, calculate_energy_gradients=True, calculate_hessian=True)
# print the energy. You can print extract properties from each molecule object, such as energy gradients and Hessian
print(molDB[0].energy)
print(molDB[1].energy)
print(molDB[1].energy-molDB[0].energy)
上述例子使用MNDO程序接口进行了测试。如果您使用的是MLatom@XACS云平台,使用的则是SCINE Sparrow的接口,因此得到的数值可能会略微不同。更多有关单点能计算的信息请参阅 教程 。
几何优化
基态闭壳层分子的几何优化和单点计算一样简单,只需要4行MLatom输入文件 opt.inp :
AIQM1
xyzfile=opt.xyz
optxyz=final_geo.xyz
geomopt
optprog=gaussian # or optprog=ase if you choose ASE
输入需要提供分子的初始XYZ坐标 opt.xyz (可以同时提供多个分子),例如甲烷的初始构型为 opt.xyz (单位是Å):
5
C 0.0000000000 0.0000000000 0.0000000000
H 1.0870000000 0.0000000000 0.0000000000
H -0.3623333220 -1.0248334322 -0.0000000000
H -0.3623333220 0.5124167161 -0.8875317869
H -0.3623333220 0.5124167161 0.8875317869
准备好输入文件 opt.inp 和 opt.xyz 以后即可运行MLatom:
mlatom opt.inp
计算完成以后,优化好的构型保存在Gaussian或ASE的输出文件中。
如果使用的是Gaussian,各个分子的Gaussian输出会保存在 mol_1.log, mol_2.log, … 中,就像其他类型的Gaussian任务一样,用户可以在GaussianView程序中进行可视化,查看分子构型。
如果使用的是ASE,用户可以直接在 final_geo.xyz 文件中获取分子的XYZ坐标,如下所示(单位是Å):
5
C 0.00000000 0.00000000 0.00000000
H 1.08666998 -0.00000000 0.00000000
H -0.36222332 -1.02452229 -0.00000000
H -0.36222332 0.51226114 -0.88726233
H -0.36222332 0.51226114 0.88726233
在Python API中运行的代码如下:
import mlatom as ml
# Get the initial guess for the molecules to optimize
initmol = ml.data.molecule.from_xyz_file('opt.xyz')
# Choose one of the predifined (automatically recognized) methods
mymodel = ml.models.methods(method='AIQM1')
# Optimize the geometry with the choosen optimizer:
geomopt = ml.optimize_geometry(model=mymodel,
initial_molecule=initmol,
program='ASE',
maximum_number_of_steps=10000)
# Get the final geometry
final_mol = geomopt.optimized_molecule
# and its XYZ coordinates
final_mol.xyz_coordinates
# Check and save the final geometry
print('Optimized coordinates:')
print(final_mol.get_xyz_string())
final_mol.write_file_with_xyz_coordinates(filename='final_geo.xyz')
更多有关几何优化的信息请参阅 教程 。
过渡态优化
优化过渡态(TSs)的输入和几何优化非常相似,唯一不同的是将关键词 geomopt 替换为 ts 。优化过渡态需要计算Hessian所以更昂贵。目前仅支持使用Gaussian接口完成这项任务,例如,在输入文件中使用 optprog=gaussian 。以下是输入文件 ts.inp 的示例:
AIQM1
xyzfile=ts.xyz
optxyz=final_geo.xyz
ts
optprog=gaussian
需要提供过渡态的初猜XYZ坐标文件 ts.xyz ,对于周环反应:
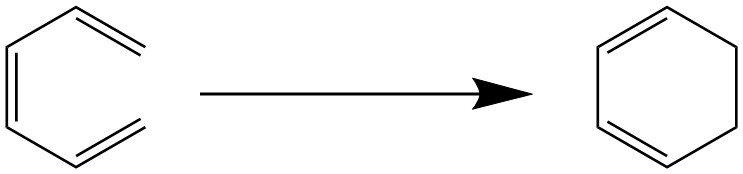
初猜如下 ts.xyz :
14
C -0.12282076 -1.09054053 1.14065341
C 0.17199635 0.23301894 1.48248953
C -0.12282076 1.35549534 0.70296425
C -0.12282076 1.35549534 -0.70296425
C 0.17199635 0.23301894 -1.48248953
C -0.12282076 -1.09054053 -1.14065341
H 0.82454258 0.40945200 2.34048883
H -0.03331673 2.33317669 1.17510642
H -0.03331673 2.33317669 -1.17510642
H 0.82454258 0.40945200 -2.34048883
H 0.43031244 -1.88602881 -1.64114758
H -1.14789312 -1.35457363 -0.93625533
H 0.43031244 -1.88602881 1.64114758
H -1.14789312 -1.35457363 0.93625533
当准备好 ts.inp 和 ts.xyz 以后即可运行MLatom进行过渡态优化:
mlatom ts.inp
计算结束以后,优化好的过渡态结构保存在XYZ坐标输出文件 final_geo.xyz 中。用户可以查看频率来判断过渡态的优化情况,即成功优化的过渡态有且仅有一个虚频,还可以使用可视化软件分析Gaussian的 .log 输出文件以查看核的运动方向。
14
6 -0.14824052 -1.18232681 1.09011331
6 0.27697295 0.08303553 1.40719277
6 -0.14824052 1.26264088 0.68226088
6 -0.14824052 1.26264088 -0.68226088
6 0.27697295 0.08303553 -1.40719277
6 -0.14824052 -1.18232681 -1.09011331
1 1.16206956 0.21862475 2.03298866
1 -0.22714441 2.21025461 1.20566513
1 -0.22714441 2.21025461 -1.20566513
1 1.16206956 0.21862475 -2.03298866
1 0.37749585 -2.04342303 -1.49163954
1 -1.19537249 -1.36555399 -0.92796582
1 0.37749585 -2.04342303 1.49163954
1 -1.19537249 -1.36555399 0.92796582
在Python API中运行的代码如下:
import mlatom as ml
# Get the initial guess for the molecules to optimize
initmol = ml.data.molecule.from_xyz_file('ts.xyz')
# Choose one of the predifined (automatically recognized) methods
mymodel = ml.models.methods(method='AIQM1')
# Optimize the geometry with the choosen optimizer:
geomopt = ml.optimize_geometry(model=mymodel,
initial_molecule=initmol,
ts=True,
program='ASE',
maximum_number_of_steps=10000)
# Get the final geometry
final_mol = geomopt.optimized_molecule
# and its XYZ coordinates
final_mol.xyz_coordinates
# Check and save the final geometry
print('Optimized coordinates:')
print(final_mol.get_xyz_string())
final_mol.write_file_with_xyz_coordinates(filename='final_geo.xyz')
参阅过渡态优化的相关 教程 以获取更多细节。
热化学计算
在MLatom的输入文件中添加频率关键词,可以在AIQM1水平上计算基态闭壳分子的热化学性质,输入文件 freq.inp 如下所示,这通常在AIQM1优化好的几何构型上继续运算:
AIQM1
xyzfile=freq.xyz
freq
optprog=gaussian # or optprog=ase if you choose ASE
输入需要提供分子的XYZ坐标文件 freq.xyz (可以同时提供多个分子),例如含有甲烷的XYZ坐标文件 freq.xyz (单位是Å):
5
C 0.000000 0.000000 0.000000
H 0.627580 0.627580 0.627580
H -0.627580 -0.627580 0.627580
H 0.627580 -0.627580 -0.627580
H -0.627580 0.627580 -0.627580
当准备好 freq.inp 和 freq.xyz 以后即可运行MLatom:
mlatom freq.inp > freq.out
计算结束以后,MLatom的输出 freq.out 中将包含0 K时分子的原子化焓、0 K时的零点振动专属原子化能、298 K时的生成热。
如果使用的Gaussian,每个分子的频率计算的输出将分别保存在 mol_1.log 、 mol_2.log … 等文件中;这些文件包含零点振动能和多种热化学性质,例如熵和吉布斯自由能。MLatom的输出将包含上述信息,以下是甲烷输出文件的例子:
Standard deviation of NN contribution : 0.00025608 Hartree 0.16069 kcal/mol
NN contribution : 0.00958812 Hartree
Sum of atomic self energies : -33.60470494 Hartree
ODM2* contribution : -6.86968756 Hartree
D4 contribution : -0.00010193 Hartree
Total energy : -40.46490632 Hartree
Atomization enthalpy at 0 K : 391.58894 kcal/mol
ZPE exclusive atomization energy at 0 K : 419.90907 kcal/mol
Heat of formation at 298.15 K : -17.30543 kcal/mol
如果使用ASE计算热化学性质时,用户需要使用 ase.linear 和 ase.symmetrynumber 这两个关键词。对于非线性分子, ase.linear 设置为0;对于线性分子, ase.linear 设置为1。 ase.symmetrynumber 是每个分子的旋转对称数,(参见C. Cramer的《Essentials of Computational Chemistry》第二版中的表10.1和附录B)。例如,对于氢气和甲烷这两个分子而言,应该设置 ase.linear=1,0 以及 ase.symmetrynumber=2,12 。
Python API为使用更复杂的模型和构建自定义的工作流程提供了更多灵活性。下面是一个几何优化和计算频率的工作流程:
import mlatom as ml
# Get the initial guess for the molecules to optimize
initmol = ml.data.molecule.from_xyz_file('freq.xyz')
# Choose one of the predifined (automatically recognized) methods
mymodel = ml.models.methods(method='AIQM1')
# Optimize the geometry with the choosen optimizer:
geomopt = ml.optimize_geometry(model=mymodel,
initial_molecule=initmol,
program='ASE',
maximum_number_of_steps=10000)
# Get the optimized molecule
final_mol = geomopt.optimized_molecule
# Do vibration analysis and thermochemistry calculation
freq = ml.thermochemistry(model=mymodel,
molecule=final_mol,
program='ASE')
# or vibration analysis only
# freq = ml.freq(model=mymodel, molecule=final_mol, program='')
# Save the molecule with vibration analysis and thermochemistry results
final_mol.dump(filename='final_mol.json',format='json')
# Check vibration analysis
print("Mode Frequencies Reduced masses Force Constants")
print(" (cm^-1) (AMU) (mDyne/A)")
for ii in range(len(final_mol.frequencies)):
print("%d %13.4f %13.4f %13.4f"%(ii,final_mol.frequencies[ii],final_mol.reduced_masses[ii],final_mol.force_constants[ii]))
# Check thermochemistry results
print(f"Zero-point vibrational energy: {final_mol.ZPE} Hartree")
print(f"Enthalpy at 298 K: {final_mol.H} Hartree")
print(f"Gibbs Free energy at 298 K: {final_mol.G} Hartree")
print(f"Heat of formation at 298 K: {final_mol.DeltaHf298} Hartree")
关于频率和热化学计算的更多细节参见相关 教程 。
半经验程序的特殊输入
你需要使用 QMprogramKeywords
有时您可能需要通过MNDO或Sparrow程序来更改AIQM1的半经验量子力学部分。因此,MLatom支持通过 QMprogramKeywords=[带有MNDO或Sparrow关键字的文件名] 读取用户定义的MNDO或Sparrow关键字,这些关键字将传递给MNDO程序。由于此前版本的原因,MNDO程序也支持 mndokeywords 。请查阅MNDO程序手册中可用的关键字。
备注
无论何时为MNDO指定特殊关键词, iop=-22 immdp=-1 nsav15=3 igeom=1 iform=1 都是必须的,指定特殊关键词时AIQM1计算只能对XYZ文件中的单个分子运行。
带电物种和自由基的计算
例如,我们想对质子化水 H3O+进行几何优化,你可以使用以下MLatom输入: optcs.inp
AIQM1
xyzfile=optcs.xyz
optxyz=final_geo.xyz
geomopt
optprog=ase
charges=1
类似地,对于自由基,您可以提供关键字 multiplicities 。
输入要求提供待优化分子的初始XYZ坐标 optcs.xyz ,如下所示(单位是Å):
4
O 0.00000000 0.00000000 0.08727273
H 0.00000000 0.90509668 -0.23272727
H -0.78383672 -0.45254834 -0.23272727
H 0.78383672 -0.45254834 -0.23272727
当准备好输入文件 optcs.inp 和 optcs.xyz 以后即可运行MLatom:
mlatom optcs.inp
输出的构型保存在 final_geo.xyz 文件中,如下所示(单位是Å):
4
O 0.00000000 -0.00000000 0.12401796
H 0.00000000 0.90385318 -0.24497568
H -0.78275982 -0.45192659 -0.24497568
H 0.78275982 -0.45192659 -0.24497568
如果想使用以上优化好的 H3O+构型计算生成热,你可以使用以下输入文件: freqcs.inp
AIQM1
xyzfile=final_geo.xyz
freq
optprog=ase
charges=1
在使用 mlatom freqcs.inp > freqcs.out 运行MLatom以后,你可以在输出中得到生成热,如下所示:
Heat of formation at 298.15 K : 150.84947 kcal/mol
* Warning * Heat of formation have high uncertainty!
垂直激发能
例如,我们想计算乙烯 1B1u 态的垂直激发能,可以使用以下MLatom输入 vee.inp :
AIQM1
xyzfile=vee.xyz
mndokeywords=mndokw
yestfile=enest.dat
输入需要提供分子的XYZ坐标 vee.xyz ,如下所示(单位为Å):
6
Ethene 1B1u
C 0.000000 0.000000 0.668188
C 0.000000 0.000000 -0.668188
H 0.000000 0.923274 1.238289
H 0.000000 -0.923274 1.238289
H 0.000000 0.923274 -1.238289
H 0.000000 -0.923274 -1.238289
以及MNDO关键词文件 mndokw :
iop=-22 immdp=-1 +
igeom=1 iform=1 +
jop=-2 nsav15=3 +
kci=5 ici1=1 ici2=1 iroot=2 ioutci=2 +
movo=-1 nciref=1 mciref=3 levexc=2
在准备好输入文件 vee.inp 、 vee.xyz 和 mndokw 后即可运行MLatom:
mlatom vee.inp
垂直激发能的输出保存在MNDO程序的输出文件 mndo.out 中,如下所示:
State 2, Mult. 1, B1u (4), E-E(1)= 7.910791 eV, E= -304.054934 eV
See also tutorial.
激发态几何优化
例如,我们想对甲醛的 1nπ*激发态( 1A” )进行几何优化,则可以使用以下输入: optes.inp
AIQM1
xyzfile=optes.xyz
optxyz=final_geo.xyz
geomopt
optprog=ase
mndokeywords=mndokw_es
输入需要提供待优化分子的初始XYZ坐标 optes.xyz ,如下所示(单位是Å):
4
formaldehyde 1npi*
C -0.02667227 0.64339915 -0.00000000
O -0.02667227 -0.71674790 0.00000000
H 0.18670592 0.93679416 1.04362466
H 0.18670592 0.93679416 -1.04362466
以及MNDO的关键词文件 mndokw_es :
iop=-22 immdp=-1 +
igeom=1 iform=1 +
jop=-2 nsav15=3 +
kharge=0 imult=0 +
kci=5 ici1=6 ici2=4 jci1=1 jci2=1 ncisym=2 +
movo=-1 nciref=1 mciref=3 levexc=2 iroot=1 lroot=1
mndokw_es 文件的第一行请求使用ODM2*哈密顿量(您不需要修改它),第二行指定几何构型以XYZ格式给出,第三行请求计算梯度并且将梯度和能量保存在 fort.15 文件中(需要先进行几何优化),第四行设置电荷(kharge=0)和多重度(imult=0),下面几行设置激发态的计算类型。 kci=5 指定GUGA-CI方法进行激发态计算; ici1 和 ici2 分别定义活跃的占据轨道数和非占据轨道数; jci1 和 jci2 定义活性空间中已占据和未占据的pi-分子轨道数; ncisym 定义态的对称性。这里,初始几何构型为 Cs点群,存在A’和A”两种不可约表示,我们使用 ncisym=2 来计算 1A” 态。 nciref 和 mciref 分别定义参考占据数目和参考占据的定义; levexc 定义最大激发能级, iroot 和 lroot 是计算的最低CI状态数和感兴趣的CI状态数。
在准备好输入文件 optes.inp 、 optes.xyz 和 mndokw_es 后即可运行MLatom:
mlatom optes.inp
输出的构型保存在 final_geo.xyz 文件中,如下所示(单位是Å):
4
C -0.10906735 0.55934608 -0.00000000
O -0.02784720 -0.77782274 0.00000000
H 0.22849093 1.00935811 0.92370071
H 0.22849093 1.00935811 -0.92370071
分子轨道可视化
如果用户使用Sparrow来提供ODM2*部分的计算:vmo_sparrow.inp, sp.xyz
AIQM1
qmprog=sparrow
xyzfile=sp.xyz
yestfile=enest.dat
QMprogramKeywords=SparrowKW
需要使用 QMprogramKeywords 关键词,以Molden波函数格式输出轨道。 SparrowKW 文件的内容应该为 -W 。计算结束以后会生成 wavefunction.molden.input 文件。您可以使用 Jmol 或者 MOLDEN 程序来打开并查阅轨道。对于Jmol程序,为得到轨道图片,您应该在面板中右键选择 Surface 和 MO 。对于MOLDEN程序,为得到轨道图片,您需要在控制面板上选择Dens. 模式,点击 Orbital 按钮,然后选择 Space 选项来设置等高线值。此外,还可以使用Chemcraft来可视化轨道,但是需要使用 .molden 后缀重命名文件。
如果用户使用MNDO提供ODM2*部分的计算: vmo_mndo.inp, sp.xyz
AIQM1
qmprog=mndo
xyzfile=sp.xyz
yestfile=enest.dat
mndokeywords=mndokw_vmo
用户应当提供含有MNDO的关键词的文件 mndokw_vmo 并添加额外的关键词 nsav13=2 :
iop=-22 immdp=-1 +
igeom=1 iform=1 +
jop=-1 nsav15=3 +
kharge=0 imult=0 nsav13=2
然后会生成 molden.dat 文件。您同样可以使用Jmol或者MOLDEN程序对轨道进行可视化。
引用
如果您使用了AIQM1,在您的出版物中可以有以下引用:
AIQM1: P. Zheng, R. Zubatyuk, W. Wu, O. Isayev, P. O. Dral. Artificial Intelligence-Enhanced Quantum Chemical Method with Broad Applicability. Nat. Commun. 2021, 12, 7022. DOI: 10.1038/s41467-021-27340-2.
MLatom: Pavlo O. Dral, Fuchun Ge, Yi-Fan Hou, Peikun Zheng, Yuxinxin Chen, Mario Barbatti, Olexandr Isayev, Cheng Wang, Bao-Xin Xue, Max Pinheiro Jr, Yuming Su, Yiheng Dai, Yangtao Chen, Lina Zhang, Shuang Zhang, Arif Ullah, Quanhao Zhang, Yanchi Ou. MLatom 3: A Platform for Machine Learning-enhanced Computational Chemistry Simulations and Workflows. J. Chem. Theory Comput. 2024, 20, 1193–1213. DOI: 10.1021/acs.jctc.3c01203.
MLatom: Pavlo O. Dral, Fuchun Ge, Yi-Fan Hou, Peikun Zheng, Yuxinxin Chen, Bao-Xin Xue, Max Pinheiro Jr, Yuming Su, Yiheng Dai, Yangtao Chen, Shuang Zhang, Lina Zhang, Arif Ullah, Quanhao Zhang, Yanchi Ou. MLatom: A Package for Atomistic Simulations with Machine Learning, version [add version number], Xiamen University, Xiamen, China, 2013–2024. MLatom.com.
ODM2* Hamiltonian: P. O. Dral, X. Wu, W. Thiel, J. Chem. Theory Comput. 2019, 15, 1743.
如果您使用MNDO程序:
MNDO program: W. Thiel,
MNDO[您使用的版本] (Max-Planck-Institut fur Kohlenforschung, Mulheim an der Ruhr, [年份])如果您使用MLatom@XACS云计算平台,使用了SCINE Sparrow:
F. Bosia, T. Husch, C. H. Müller, S. Polonius, J.-G. Sobez, M. Steiner, J. P. Unsleber, A. C. Vaucher, T. Weymuth, M. Reiher,
qcscine/sparrow: to-be-released alpha version with modifications by P. Zheng, 2022.T. Husch, A. C. Vaucher, M. Reiher, Int. J. Quantum Chem. 2018, 118, e25799.
D4: E. Caldeweyher, C. Bannwarth, S. Grimme, J. Chem. Phys. 2017, 147, 034112.
D4 program: E. Caldeweyher, S. Ehlert, S. Grimme, DFT-D4, Version [您使用的版本], (Mulliken Center for Theoretical Chemistry, University of Bonn, [年份])
ANI model: J. S. Smith, O. Isayev, A. E. Roitberg, Chem. Sci. 2017, 8, 3192
TorchANI program: X. Gao, F. Ramezanghorbani, O. Isayev, J. S. Smith, A. E. Roitberg, J. Chem. Inf. Model. 2020, 60, 3408