频率和热化学
在本教程中,我们将展示如何使用MLatom计算分子的频率。我们在 几何优化 的基础上继续本次教程,因为通常先进行几何优化,然后计算频率,即检查优化结果是能量最小值点还是过渡态(虚频数目),并获得ZPVE和其他热化学校正。
警告
We recommend to use UAIQM methods for these calculations, example below is just to show that you can use other methods too.
以下是使用XACS云计算平台和Python API进行频率和热化学计算的演示视频:
我们使用与几何优化相同的例子。在频率计算前,通常需要进行几何优化,并且对两者应该使用相同的方法或模型。
在获得优化好的几何构型后(opt.xyz)。如 几何优化 中所述,用户可以使用输入文件或命令行选项 freq.inp 来进行频率计算。如下所示(参见 通过Python API计算频率 的部分):
freq # 1. requests frequency calculation
ANI-1ccx # 2. pre-trained model, the same as that used in geometry optimization
xyzfile=opt.xyz # 3. file with optimized geometry
与几何优化类似,用户需要提供QM、ML或QM/ML结合的模型或者方法。解析Hessian在可用时使用,否则可以使用半解析(用解析梯度计算)或全数值Hessian(只用能量计算)。
xyzfile=[文件名] 告诉MLatom在哪个文件中提取几何构型。用户可以直接使用MLatom优化的构型(文件由 optxyz 关键字定义),或者由用户以XYZ格式提供。例如在本例中(以Å为单位, opt.xyz ),此文件如下所示:
9
C -1.2121068029534 -0.2252488537660 0.0000164117920
H -1.2701429633537 -0.8599818439347 -0.8855315546559
H -1.2701264459840 -0.8599834499240 0.8855643352209
H -2.0710636368970 0.4504289041619 0.0000252076803
C 0.0804149514179 0.5556635798575 0.0000041512523
H 0.1395635927681 1.1970970820212 -0.8856250576131
H 0.1395848675981 1.1970854779804 0.8856411245403
O 1.1428329343502 -0.3971737931938 -0.0000106635278
H 1.9796722202817 0.0702558186994 -0.0001121252171
当用户创建输入文件以后,即可运行MLatom,例如在XACS云平台上运行:
mlatom freq.inp &> freq.out
运行结果将保存在 freq.out 中。
或者,用户也可以在命令行中进行相同的模拟:
mlatom freq ANI-1ccx xyzfile=opt.xyz
用户能够在MLatom的输出中找到振动分析和热化学结果。振动分析输出每个简振模式的频率、约化质量和力常数。热化学部分输出零点能、焓、吉布斯自由能、生成热和其他性质。在本示例中,输出如下所示:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
Rotational symmetry number: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 261.0407 1.0929 0.0439
2 286.9474 1.1295 0.0548
3 428.0328 2.7260 0.2943
4 841.1644 1.0947 0.4564
5 928.2688 2.3346 1.1853
6 1082.6338 3.1779 2.1946
7 1138.6399 1.9583 1.4959
8 1212.5257 1.5518 1.3442
9 1287.5002 1.1134 1.0874
10 1292.8263 1.0682 1.0520
11 1426.7497 1.2307 1.4760
12 1457.4408 1.3203 1.6524
13 1496.9454 1.1496 1.5178
14 1501.2654 1.0458 1.3887
15 1524.8936 1.0529 1.4426
16 3063.7060 1.0530 5.8232
17 3076.9020 1.1120 6.2026
18 3093.2039 1.0342 5.8299
19 3201.4189 1.1000 6.6424
20 3213.8757 1.1004 6.6964
21 3741.4822 1.0681 8.8098
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NNs : 0.00063190 Hartree 0.39652 kcal/mol
Energy : -154.89195912 Hartree
ZPE-exclusive internal energy at 0 K: -154.89196 Hartree
Zero-point vibrational energy : 0.08101 Hartree
Internal energy at 0 K: -154.81095 Hartree
Enthalpy at 298 K: -154.80576 Hartree
Gibbs free energy at 298 K: -154.83631 Hartree
Atomization enthalpy at 0 K: 1.21200 Hartree 760.54458 kcal/mol
ZPE-exclusive atomization energy at 0 K: 1.29301 Hartree 811.37653 kcal/mol
Heat of formation at 298 K: -0.09030 Hartree -56.66187 kcal/mol
备注
MLatom会把分子对象转储到名为 freq[molecule number].json 的json文件中。每个分子的json文件包含频率计算的信息,如简正模、频率、热化学数据。
Visualizing vibrations
There are several ways to visualize the vibrations:
Currently only on the XACS cloud computing:
At the end of the calculations via input file/command line using the options
freq,ir, orraman, MLatom will dump thefreq_gaussian{mol_index}.logfile, which uses Gaussian-style output format for frequencies. You can open it in ChemCraft.You can also dump text output file using Gaussian-style format for frequencies from the Python API:
mymolecule.dump(filename='gauss.log', format='gaussian').
You can directly view the vibrations in
Jupyter notebookby usingmymolecule.view(normal_mode=...), as shown below for an examplemolvibr.jsonfile:
import mlatom as ml
# let's load the molecule with the required properties
molvibr = ml.molecule()
molvibr.load(filename='molvibr.json')
# choose the normal mode to visualize
normal_mode = 1
# let's view it
molvibr.view(normal_mode=normal_mode)
You appear to be running in JupyterLab (or JavaScript failed to load for some other reason). You need to install the 3dmol extension:
jupyter labextension install jupyterlab_3dmol
# we can also check the information for this normal mode
print(f'Frequency: {molvibr.frequencies[normal_mode]:.2f} cm^-1')
print(f'Normal mode in Angstrom')
for atom in molvibr.atoms:
disp = atom.normal_modes[normal_mode]
print(f" {disp[0]:8.3f} {disp[1]:8.3f} {disp[2]:8.3f}")
Frequency: 288.70 cm^-1
Normal mode in Angstrom
-0.000 0.000 -0.025
-0.085 0.168 -0.141
0.085 -0.168 -0.141
0.000 0.000 0.184
-0.000 -0.000 -0.003
0.018 -0.021 -0.014
-0.018 0.021 -0.014
0.000 0.000 0.085
-0.000 -0.000 -0.890
# the non-displaced geometry for reference
print(molvibr.get_xyz_string())
9 C -1.2121068000000 -0.2252488500000 0.0000164100000 H -1.2701429600000 -0.8599818400000 -0.8855315500000 H -1.2701264500000 -0.8599834500000 0.8855643400000 H -2.0710636400000 0.4504289000000 0.0000252100000 C 0.0804149500000 0.5556635800000 0.0000041500000 H 0.1395635900000 1.1970970800000 -0.8856250600000 H 0.1395848700000 1.1970854800000 0.8856411200000 O 1.1428329300000 -0.3971737900000 -0.0000106600000 H 1.9796722200000 0.0702558200000 -0.0001121300000
# non-displaced geometry
molvibr.view()
You appear to be running in JupyterLab (or JavaScript failed to load for some other reason). You need to install the 3dmol extension:
jupyter labextension install jupyterlab_3dmol
选择方法或模型
MLatom为用户提供了多种方法和模型。如上所示,MLatom可以自动识别许多方法如ANI-1ccx或AIQM1。我们还展示了使用QM方法(B3LYP/6-31G*)和用户训练的机器学习模型(ANI模型)的示例。
定义QM方法的一般方法是使用 method 和相应的QM程序(MLatom使用这些程序的接口)。例如,使用B3LYP/6-31G*的输入文件如下所示:
freq # 1. requests frequency calculation
method=B3LYP/6-31G* # 2. requests running DFT calculation with B3LYP
qmprog=PySCF # 3. requests using PySCF for B3LYP calculations; qmprog=Gaussian can also be used
xyzfile=opt.xyz # 4. file with optimized geometry
使用用户训练的机器学习模型进行频率计算的一般方法是使用 MLmodelType 和 MLmodelIn 关键字来指定模型类型。例如,使用ANI模型的输入文件为:
freq # 1. requests frequency calculation
MLmodelType=ANI # 2. request optimization with the ANI-type of machine learning potential
MLmodelIn=ani.npz # 3. the file with the trained model should be provided, here it is ani.npz file
xyzfile=opt.xyz # 4. file with optimized geometry
用户定义的混合模型,如delta-learning模型,只能通过Python API用于频率计算, 此处 对其进行了演示。
备注
原则上,我们建议使用AIQM1,因为该方法通常是一定成本下最准确的方法。但目前仅适用于含有CHNO元素的化合物。另外,为了使其更好地得到运用,建议为其QM部分安装MNDO程序。XACS云平台使用的是Sparrow,它目前只提供数值梯度,而Hessians严重限制了它对频率计算的适用性。因此,改用ANI-1ccx是XACS云平台的一个很好的替代方案(它对基态中性闭壳层化合物有额外的限制)。
而且,在ML模型中,Hessians目前只适用于ANI系列的模型。
多个分子的计算
与几何优化类似,MLatom可以进行多个分子的频率计算。MLatom将输出每个分子的振动分析和热化学性质。要进行这些计算,用户仅需准备具有多个分子几何构型的XYZ文件(或从此前MLatom的几何优化中获取此文件),例如,对于氢气和甲烷分子, opt.xyz 文件如下所示:
2
1 0.0000000000 0.0000000000 0.0000000000
1 0.7414000000 0.0000000000 0.0000000000
5
C 0.0000000000 0.0000000000 0.0000000000
H 1.0870000000 0.0000000000 0.0000000000
H -0.3623333220 -1.0248334322 -0.0000000000
H -0.3623333220 0.5124167161 -0.8875317869
H -0.3623333220 0.5124167161 0.8875317869
电荷和多重度
定义单个或多个分子的电荷和多重度,其输入如下所示:
freq # 1. requests frequency calculation
AIQM1 # 2. AI-enhanced quantum mechanical method 1
xyzfile=opt.xyz # 3. file with optimized geometries
charges=0,1 # 4. charge of the first molecule is 0, of the second is 1.
multiplicities=1,2 # 5. multiplicity of the first molecule is 1, second - 2
备注
对于像ANI-1ccx这样在中性闭壳层分子中训练的模型而言,定义电荷和多重度是没有意义的。
选择程序
MLatom提供了几种计算频率和热化学性质的方法(程序),与几何优化类似,用户可以使用 freqprog 关键字选择程序。有三个选项可用: freqprog=Gaussian , freqprog=PySCF 和 freqprog=ASE 指定使用相应的程序。
这些实际上是不同的任务,虽然它们在Python API中是分开的( 如下所示 ),但在输入文件中,当使用 freq 关键字时,两个任务都会执行。
freqprog=Gaussian 使用Gaussian运行这两项任务,并生成可供用户修改和检查的输入和输出文件。Gaussian是一款非常稳定且被广泛使用的软件,但在XACS云平台上不可用,需要用户在本地安装。
freqprog=PySCF 将使用PySCF来生成热化学性质,这样十分稳健,因为PySCF是一个开源的Python包,所以也可以在XACS云平台上使用。
如果使用 freqprog=ASE ,则使用ASE进行频率计算后的热化学性质计算,该程序使用基于TorchANI(修改为正确捕获过渡态中的虚频)的改进代码。修改后的TorchANI代码给出的频率也经过了我们的测试,可在XACS云平台上使用。
如果没有提供 freqprog ,默认情况下,MLatom将检查Gaussian是否可用,如果可用则使用Gaussian,否则将使用PySCF,ASE和修改后的TorchANI代码。
选用程序时,请参阅以下说明:
ASE
对于3.1.1以前的MLatom版本,用户应该使用 ase.linear 关键字来告诉ASE分子是否为线性的。该关键字默认值为0,代表非线性分子;若分子为线性,此关键字的值应设为1。若输入的XYZ文件中有多个分子,设置 ase.linear=1 可使MLatom假定它们均为线性分子。或者,用户可使用 ase.linear=1,0 为不同分子指定不同线性。对于3.1.1及更新的版本,MLatom可以自动检测分子的线性,无需用户指定。但若有需要,用户仍可自行指定分子线性,MLatom将使用用户指定的内容进行计算。
另一重要该关键字是 ase.symmetrynumber,可指定分子的对称性。MLatom中的默认值对应 \(C_1\) 点群。用户可参考下表定义对称数,下表摘自C. Cramer的《Essentials of Computational Chemistry》第二版。
点群 |
对称数 |
|---|---|
\(C_1\) |
\(1\) |
\(C_i\) |
\(1\) |
\(C_s\) |
\(1\) |
\(C_{{\infty}v}\) |
\(1\) |
\(D_{{\infty}h}\) |
\(2\) |
\(S_n,n=2,4,6,...\) |
\(n/2\) |
\(C_n,n=2,3,4,...\) |
\(n\) |
\(C_{nh},n=2,3,4,...\) |
\(n\) |
\(C_{nv},n=2,3,4,...\) |
\(n\) |
\(D_n,n=2,3,4,...\) |
\(2n\) |
\(D_{nh},n=2,3,4,...\) |
\(2n\) |
\(D_{nd},n=2,3,4,...\) |
\(2n\) |
\(T\) |
\(12\) |
\(T_d\) |
\(12\) |
\(O_h\) |
\(24\) |
\(I_h\) |
\(60\) |
例如,如果用户输入的XYZ文件有氢气(属于 \(D_{{\infty}h}\) 群)和甲烷(属于 \(T_d\) 群),则输入文件如下所示:
freq
ANI-1ccx
xyzfile=opt.xyz
freqprog=ase
ase.linear=1,0
ase.symmetrynumber=2,12
Gaussian
使用Gaussian时会输出 gaussian.log 文件,它与普通的Gaussian输出文件类似,不同之处在于它使用MLatom的模型来预测Hessian以进行频率计算。接下来,您可以使用您喜欢的工具来分析这个输出,这对于Gaussian用户来说是一个很大的优势。以下是用Gaussian计算频率的输入文件:
freq
ANI-1ccx
xyzfile=opt.xyz
freqprog=Gaussian
对于上述例子,MLatom的输出文件如下所示:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 264.1253 1.0872 0.0447
2 288.7816 1.1305 0.0555
3 429.1248 2.7295 0.2961
4 840.9571 1.0959 0.4566
5 929.0118 2.3254 1.1825
6 1083.2419 3.1763 2.1960
7 1138.7381 1.9666 1.5025
8 1211.7614 1.5471 1.3384
9 1291.9096 1.0694 1.0516
10 1299.4679 1.1131 1.1074
11 1434.7836 1.2319 1.4941
12 1464.0813 1.3257 1.6743
13 1497.4787 1.1427 1.5097
14 1502.1301 1.0457 1.3902
15 1525.4126 1.0539 1.4449
16 3045.3746 1.0531 5.7544
17 3061.9747 1.1130 6.1482
18 3092.9313 1.0343 5.8295
19 3197.6062 1.0999 6.6261
20 3213.0380 1.1000 6.6905
21 3741.0501 1.0681 8.8073
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NNs : 0.00062817 Hartree 0.39419 kcal/mol
Energy : -154.89196013 Hartree
ZPE-exclusive internal energy at 0 K: -154.89196 Hartree
Zero-point vibrational energy : 0.08100 Hartree
Internal energy at 0 K: -154.81096 Hartree
Enthalpy at 298 K: -154.80578 Hartree
Gibbs free energy at 298 K: -154.83631 Hartree
Atomization enthalpy at 0 K: 1.21202 Hartree 760.55134 kcal/mol
ZPE-exclusive atomization energy at 0 K: 1.29301 Hartree 811.37710 kcal/mol
Heat of formation at 298 K: -0.09032 Hartree -56.67409 kcal/mol
此处可下载完整的 MLatom 和 Gaussian 输出文件。
另外,用户可以修改 gaussian.com 文件,其中包含使用MLatom模型进行几何优化所需的输入。
在修正 gaussian.com 文件后,用户可以如常运行Gaussian,例如,在系统中使用 g16 gaussian.com 命令行。
PySCF
PySCF的频率计算工作原理与Gaussian相似。我们对源代码进行了一些修改,使其适应MLatom。通过使用如下输入:
freq
ANI-1ccx
xyzfile=opt.xyz
freqprog=PySCF
可以得到如下所示的MLatom的输出文件:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 263.8939 1.0878 0.0446
2 288.6910 1.1303 0.0555
3 429.0255 2.7312 0.2962
4 840.8114 1.0961 0.4566
5 928.7823 2.3273 1.1829
6 1082.9072 3.1819 2.1984
7 1138.4541 1.9665 1.5017
8 1211.4647 1.5472 1.3379
9 1291.7699 1.0696 1.0516
10 1299.3247 1.1131 1.1072
11 1434.5579 1.2319 1.4937
12 1463.8316 1.3262 1.6743
13 1497.2788 1.1422 1.5087
14 1501.9697 1.0458 1.3901
15 1525.2540 1.0541 1.4448
16 3045.0585 1.0532 5.7540
17 3061.5892 1.1131 6.1473
18 3092.6304 1.0344 5.8292
19 3197.1933 1.1000 6.6252
20 3212.6500 1.1001 6.6896
21 3740.7180 1.0683 8.8072
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NNs : 0.00062817 Hartree 0.39419 kcal/mol
Energy : -154.89196013 Hartree
ZPE-exclusive internal energy at 0 K: -154.89196 Hartree
Zero-point vibrational energy : 0.08098 Hartree
Internal energy at 0 K: -154.81098 Hartree
Enthalpy at 298 K: -154.80579 Hartree
Gibbs free energy at 298 K: -154.83632 Hartree
Atomization enthalpy at 0 K: 1.21203 Hartree 760.55897 kcal/mol
ZPE-exclusive atomization energy at 0 K: 1.29301 Hartree 811.37718 kcal/mol
Heat of formation at 298 K: -0.09033 Hartree -56.68121 kcal/mol
使用Python API进行计算
Python API为使用更复杂的模型和构建自定义工作流提供了更大的灵活性。
Below is a workflow of optimizing geometry and calculating frequency (see Jupyter notebook):
import mlatom as ml
# Get the initial guess for the molecules to optimize
initmol = ml.data.molecule.from_xyz_string(''' 9
C -1.2121068029534 -0.2252488537660 0.0000164117920
H -1.2701429633537 -0.8599818439347 -0.8855315546559
H -1.2701264459840 -0.8599834499240 0.8855643352209
H -2.0710636368970 0.4504289041619 0.0000252076803
C 0.0804149514179 0.5556635798575 0.0000041512523
H 0.1395635927681 1.1970970820212 -0.8856250576131
H 0.1395848675981 1.1970854779804 0.8856411245403
O 1.1428329343502 -0.3971737931938 -0.0000106635278
H 1.9796722202817 0.0702558186994 -0.0001121252171''')
# Choose one of the predifined (automatically recognized) methods
mymodel = ml.models.methods(method='ANI-1ccx')
/mlatom/software/miniconda3/lib/python3.11/site-packages/torchani/resources/ /mlatom/software/miniconda3/lib/python3.11/site-packages/torchani/resources/
# Optimize the geometry with the choosen optimizer:
geomopt = ml.optimize_geometry(model=mymodel, initial_molecule=initmol, program='ASE', maximum_number_of_steps=10000)
# Get the optimized molecule
final_mol = geomopt.optimized_molecule
print(final_mol.get_xyz_string())
9 C -1.2121068000000 -0.2252488500000 0.0000164100000 H -1.2701429600000 -0.8599818400000 -0.8855315500000 H -1.2701264500000 -0.8599834500000 0.8855643400000 H -2.0710636400000 0.4504289000000 0.0000252100000 C 0.0804149500000 0.5556635800000 0.0000041500000 H 0.1395635900000 1.1970970800000 -0.8856250600000 H 0.1395848700000 1.1970854800000 0.8856411200000 O 1.1428329300000 -0.3971737900000 -0.0000106600000 H 1.9796722200000 0.0702558200000 -0.0001121300000
# Do vibration analysis and thermochemistry calculation
freq = ml.thermochemistry(model=mymodel, molecule=final_mol, program='PySCF')
# or vibration analysis only
# freq = ml.freq(model=mymodel, molecule=final_mol, program='')
# Save the molecule with vibration analysis and thermochemistry results
final_mol.dump(filename='molvibr.json',format='json')
# Check vibration analysis
print("Mode Frequencies Reduced masses Force Constants")
print(" (cm^-1) (AMU) (mDyne/A)")
for ii in range(len(final_mol.frequencies)):
print("%d %13.4f %13.4f %13.4f"%(ii,final_mol.frequencies[ii],final_mol.reduced_masses[ii],final_mol.force_constants[ii]))
# Check thermochemistry results
print(f"Zero-point vibrational energy: {final_mol.ZPE} Hartree")
print(f"Enthalpy at 298 K: {final_mol.H} Hartree")
print(f"Gibbs Free energy at 298 K: {final_mol.G} Hartree")
print(f"Heat of formation at 298 K: {final_mol.DeltaHf298} Hartree")
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
0 263.8585 1.0877 0.0446
1 288.6962 1.1303 0.0555
2 429.0266 2.7312 0.2962
3 840.8100 1.0961 0.4566
4 928.7816 2.3273 1.1829
5 1082.9074 3.1819 2.1985
6 1138.4535 1.9665 1.5017
7 1211.4598 1.5473 1.3379
8 1291.7733 1.0696 1.0516
9 1299.3241 1.1131 1.1072
10 1434.5579 1.2319 1.4937
11 1463.8294 1.3261 1.6742
12 1497.2782 1.1422 1.5087
13 1501.9029 1.0458 1.3899
14 1525.2521 1.0541 1.4448
15 3045.0578 1.0532 5.7540
16 3061.5866 1.1131 6.1473
17 3092.6302 1.0344 5.8292
18 3197.2113 1.1000 6.6252
19 3212.6491 1.1001 6.6896
20 3740.7179 1.0683 8.8072
Zero-point vibrational energy: 0.08098376608079631 Hartree
Enthalpy at 298 K: -154.8057865062314 Hartree
Gibbs Free energy at 298 K: -154.83632007673512 Hartree
Heat of formation at 298 K: -0.09032742391785184 Hartree
You can compare your results with the output shown above and obtained with the calculations through the input file.
There will be several properties related to thermochemistry listed below that are attributed to the molecule object (in Hartree for energies and Hartree/K for entropy) after calculation:
saved_dict = {#...
'ZPE': 0.080996, # Zero-point energy
'DeltaE2U': 0.085241, # Difference between internal energy and total energy (ZPVE-exclusive)
'DeltaE2H': 0.086185, # Difference between enthalpy and total energy (ZPVE-exclusive)
'DeltaE2G': 0.055654, # Difference between Gibbs free energy and total energy (ZPVE-exclusive)
'U0': -154.810964, # Internal energy at 0 K
'H0': -154.810964, # Enthalpy at 0 K
'U': -154.80672, # Internal energy at 298 K
'H': -154.805775, # Enthalpy at 298 K
'G': -154.836306, # Gibbs free energy at 298 K
'S': 0.00010240004758876359, # entropy
'atomization_energy_0K': 1.2120157100000029,
'ZPE_exclusive_atomization_energy_0K': 1.293011710000003,
'DeltaHf298': -0.0903159176864495 # Heat of formation at 298 K
}
# check out dict:
# final_mol.__dict__
You can retrieve the value of the property by directly calling molecule.property (e.g. molecule.G will return you the Gibbs free energy of the molecule).
final_mol.G
-154.83632007673512
备注
请注意, ml.thermochemistry 包含振动分析和热化学计算。如果你只想做振动分析,可以使用 ml.freq 代替。所有结果都保存在 final_mol 参数中。
使用自定义混合模型进行计算
最后是使用自定义delta-learning模型的一个更高级的例子,该模型是根据全构型相互作用和Hartree-Fock能量之间的差异进行训练的:
训练点的XYZ坐标,Full CI能量和Hartree-Fock能量可在此下载(xyz_h2_451.dat, E_FCI_451.dat, E_HF_451.dat 。用户可以尝试自行训练delta-learning模型。这里,我们提供了一个预训练的模型 delta_FCI-HF_h2.unf 。
import mlatom as ml
# Get the initial guess for the molecules to optimize
initmol = ml.data.molecule.from_xyz_file('h2_init.xyz')
# Let's build our own delta-model
# First, define the baseline QM method, e.g.,
baseline = ml.models.model_tree_node(name='baseline', operator='predict', model=ml.models.methods(method='HF/STO-3G', program='pyscf'))
# Second, define the correcting ML model, in this case the ANI model trained on the differences between full CI and HF
delta_correction = ml.models.model_tree_node(name='delta_correction', operator='predict', model=ml.models.ani(model_file='delta_FCI-HF_h2_ani.npz'))
# Third, build the delta-model which would sum up the predictions by the baseline (HF) with the correction from ML
delta_model = ml.models.model_tree_node(name='delta_model', children=[baseline, delta_correction], operator='sum')
# Optimize the geometry with the delta-model as usual:
geomopt = ml.optimize_geometry(model=delta_model, initial_molecule=initmol, program='ASE')
# Get the final geometry approximately at the full CI level
final_mol = geomopt.optimized_molecule
print('Optimized coordinates:')
print(final_mol.get_xyz_string())
final_mol.write_file_with_xyz_coordinates(filename='final.xyz')
# Let's check how many full CI calculations, our delta-model saved us
print('Number of optimization steps:', len(geomopt.optimization_trajectory.steps))
# Calculate frequency
freq = ml.freq(model=delta_model, molecule=final_mol, program='')
# Check vibration analysis
print("Mode Frequencies Reduced masses Force Constants")
print(" (cm^-1) (AMU) (mDyne/A)")
for ii in range(len(final_mol.frequencies)):
print("%d %13.4f %13.4f %13.4f"%(ii,final_mol.frequencies[ii],final_mol.reduced_masses[ii],final_mol.force_constants[ii]))
给定初始的几何构型 h2_init.xyz ,当使用上面的代码时,您将得到以下输出:
Optimized coordinates:
2
H 0.1272159900000 0.0000000000000 0.0000000000000
H 0.8727840100000 0.0000000000000 0.0000000000000
Number of optimization steps: 7
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
0 4327.2885 1.0078 11.1190
Diels-Alder反应中的热化学
通过使用这些热化学性质,用户能够很容易地评估化学行为各个方面的相对能量,例如反应过程中能量分布的变化。我们以 MLatom 3论文 中的Diels-Alder反应为例,讨论环戊二烯与马来酰亚胺的反应。您可以在这里下载所需的几何文件: re.xyz 。
re.xyz 中有3个结构:前两个结构是反应物,第三个结构是产物(见下图):
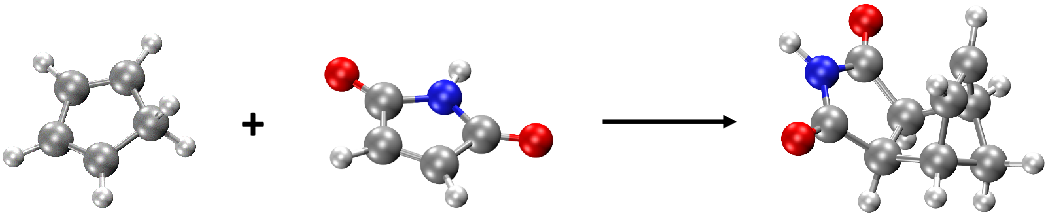
因此,基本思路是计算每个分子的热化学性质,然后计算从生成物到反应物的能量变化。我们将证明使用Python API的便捷性(同样可以使用输入文件或命令行手动完成计算,即对每个分子进行热化学计算,并获得每种类型能量的变化)。
import mlatom as ml
# read molecules from .xyz file
reDB = ml.data.molecular_database().read_from_xyz_file('re.xyz')
optreDB = ml.data.molecular_database()
# define method to calculate thermochemical properties
model = ml.models.methods(method='AIQM1', qm_program='mndo')
for mol in reDB:
# geometry optimization
geomopt = ml.optimize_geometry(model=model, initial_molecule=mol, program='gaussian')
optmol = geomopt.optimized_molecule
# frequency calculation
ml.thermochemistry(model=model, molecule=optmol)
optreDB.append(optmol)
# get relative energies
deltaE = optreDB[2].energy - optreDB[1].energy - optreDB[0].energy
deltaG = optreDB[2].G - optreDB[1].G - optreDB[0].G
deltaH = optreDB[2].H - optreDB[1].H - optreDB[0].H
print(deltaE)
print(deltaG)
print(deltaH)
以下是包含ZPVE-exclusive能量,吉布斯自由能和焓的输出的总结。
方法 |
\(\Delta E_r\) |
\(\Delta G_r\) |
\(\Delta H_r\) |
|---|---|---|---|
reference |
-34.20 |
- |
- |
AIQM1 |
-34.13 |
-15.98 |
-30.36 |
这表明如果可以使用AIQM1,则推荐使用AIQM1以快速获得准确的结果;它通常比运行类似的、较慢且较不准确的DFT计算更可取。
问题或建议
如果您有进一步的问题、批评和建议,我们很乐意通过 电子邮件 、 Slack (首选)或微信(请发送电子邮件请求将您添加到XACS用户支持组)以英文或中文接收您的意见。