UAIQM

UAIQM – Universal and Updatable Artificial Intelligence-Enhanced Quantum Mechanical Foundational Models – supercharge your quantum chemical simulations with the best accuracy for the lowest computational effort. See the preprint for details (please cite it if you run UAIQM calculations):

  • Yuxinxin Chen, Yi-Fan Hou, Olexandr Isayev, and Pavlo O. Dral. Universal and Updatable Artificial Intelligence-Enhanced Quantum Chemical Foundational Models. Preprint on ChemRxiv: https://doi.org/10.26434/chemrxiv-2024-604wb.

We provide the Jupyter notebook for users to easily run UAIQM jobs on the XACS cloud.

备注

Currently, you can only use this feature with A-MLatom and MLatom@XACS, i.e., you can only perform such calculations on the XACS cloud (registration and basic use is free but you may want to request more computing time) or request the copy of A-MLatom for your local use. It is not available yet in the open-source MLatom.

备注

If not requested otherwise, by running calculations with the UAIQM models, you agree that your calculation data might be made open access together with the UAIQM models improved by using these data. The UAIQM are updatable models meaning that they need to see your unconfident calculations to improve themselves! It means that by running UAIQM calculations you help to improve the quality of the future models – you and other users will surely benefit from it. However, we understand that you might have your super-secret molecule to calculate which you do not want to share with others. In this case, you might explore other options as described in the data policy.

What is UAIQM?

UAIQM is a platform hosting a library of foundational models ranging from universal machine learning potentials (MLPs) to quantum mechanical (QM) methods improved with neural networks. All of them can be used out-of-box without retraining while maintaining both high accuracy and low computational cost. The UAIQM methods are available across the periodic table, have gradients and hessians, and many of them other quantum chemical properties like charges and dipole moments. One of the key features of UAIQM is the auto-selection of the optimal UAIQM method for the given atomistic system and time budget. Another key feature is that UAIQM is continuously improved with more usage.

While UAIQM is applicable to a wide range of situations, it shines for the neutral, closed-shell CHNO molecules where it consistently achieves the gold-standard CCSD(T)/CBS accuracy but with a much lower cost. For other situations, it is as good or better than the underlying baseline QM method, i.e., semi-empirical GFN2-xTB or hybrid Kohn–Sham DFT ωB97X/6-31G* and ωB97X/def2-TZVPP. The baseline is chosen based on how much time the user wants to spend on the simulations.

The computational cost and robustness of UAIQM models are defined by the baseline: the fastest are universal MLP (no baseline), while the slowest have ωB97X/def2-TZVPP as the baseline. The best cost/performance tradeoff might be the semi-empirical baseline GFN2-xTB. The robustness is improved when slower and more accurate baseline is used, i.e., while in most cases fastest solution suffices, in challenging cases you might need to use a slower baseline. No worries – UAIQM tells you whether the automatically chosen method provides confident prediction. However, you are free to pick by yourself another model as described next.

_images/uaiqm_elements_20240808.png

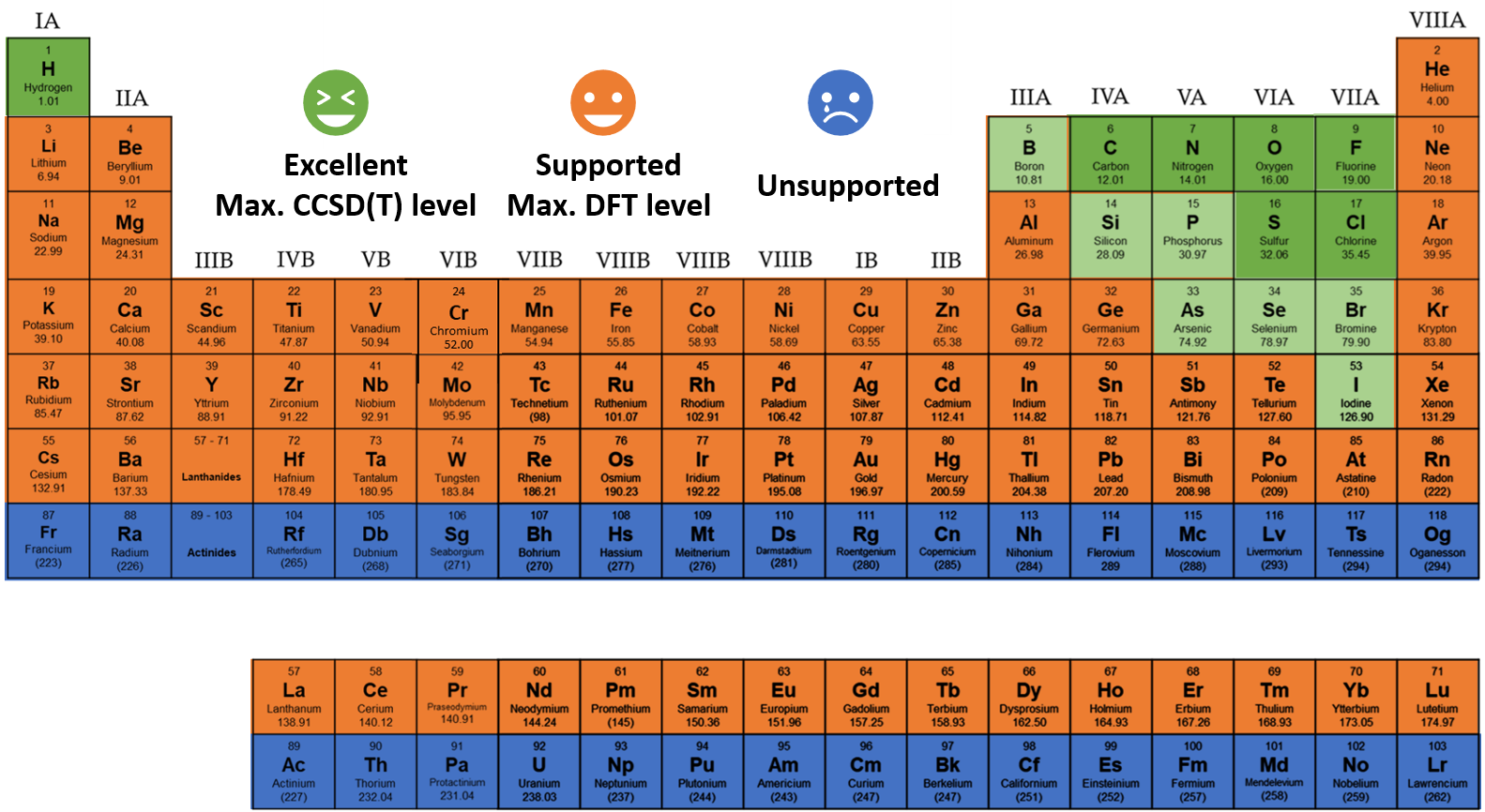
UAIQM library (June 21, 2024)

The following overview of the existing UAIQM models is useful when you want to have a better idea what model was autoselected or when you want to select the model yourself. While referring to this overview, please pay attention to:

  • baseline: defines how robust and fast your UAIQM model is. The slower, the better.

  • target: defines the level on which the UAIQM model was trained on. Auto-selection only chooses models targeting the coupled cluster (CC) accuracy at CCSD(T)/CBS. Only in rare instances you might want to try the model trained on the DFT target.

  • version: the newer, the better, but not always, see uncertainty quantification below.

  • UQ criteria: the threshold of the uncertainty quantification metric. If your calculations exceed the given threshold they must be unconfident.

keywords in MLatom (case-insensitive)

version

target level

baseline

UQ criteria (kcal/mol)

uaiqm_nobaseline@dft

20240606

DFT

-

1.28

uaiqm_nobaseline@cc (ANI-1ccx)

20190701

CC

-

1.68

uaiqm_nobaseline@cc

20240606

CC

-

0.95

uaiqm_odm2star@dft (AIQM1@DFT)

20211202

DFT

ODM2*

0.54

uaiqm_odm2star@cc (AIQM1)

20211202

CC

ODM2*

0.41

uaiqm_odm2star@cc

20240308

CC

ODM2*

0.55

uaiqm_gfn2xtbstar@dft

20240106

DFT

GFN2-xTB*

0.45

uaiqm_gfn2xtbstar@dft

20240619

DFT

GFN2-xTB*

0.68

uaiqm_gfn2xtbstar@cc

20240106

CC

GFN2-xTB*

0.36

uaiqm_wb97x631gp@cc

20230924

CC

ωB97X/6-31G*

0.49

uaiqm_wb97xdef2tzvpp@cc

20230923

CC

ωB97X/def2-TZVPP

0.32

uaiqm_wb97xdef2tzvpp@cc

20240227

CC

ωB97X/def2-TZVPP

0.26

uaiqm_wb97xdef2tzvpp@cc

20240228

CC

ωB97X/def2-TZVPP

0.3

We use PySCF for DFT, modified xTB for GFN2-xTB*, Sparrow for ODM2* and dftd4 for D4 dispersion corrections, and TorchANI for the NN part in the UAIQM models.

备注

  • uaiqm_gfn2xtbstar@dft, version 20240619 might be better for F, S, Cl-containing elements than other models based on the GFN2-xTB baseline, although it is trained on the DFT-level data.

  • models based on the ODM2* baseline are not auto-selected on the cloud because they have no analytical gradients which leads to many problems with optimizations and frequency calculations. They can be selected manually, e.g., for single-point calculations.

(Auto-)selection of UAIQM models

The first step is to choose the model. We recommend starting from the default settings for the model auto-selection as described below.

Important. Once you selected the model, it is strongly adviced to stick to this model when you perform a series of related calculations, e.g., when you calculate relative energies such as reaction energies or barriers.

Auto-selection

With atomatic selection, UAIQM library provides user with the optimal model given the chemical system, expected time budget and computational resources.

For input file, by requesting uaiqm in the first line of the input file, user can start to choose the optimal method in UAIQM library by setting keywords ncpus and time_budget for number of CPUs used and the expected time budget (s, m, h and d can be recognized, e.g. 3m.). A simple example for single-point calculation is provided:

uaiqm
time_budget=1s
ncpus=1
xyzfile='5

C         0.0000000000        0.0000000000        0.0000000000
H         1.0870000000        0.0000000000        0.0000000000
H        -0.3623333220       -1.0248334322       -0.0000000000
H        -0.3623333220        0.5124167161       -0.8875317869
H        -0.3623333220        0.5124167161        0.8875317869
'
yestfile=enest.dat

备注

Currently, auto-selection of UAIQM methods with input file only supports single molecule. If more than one molecule is provided, only the first one will be choosen to perform automatic selection.

For using python API, you need to initialize the model with mlatom.models.uaiqm(method="uaiqm_optimal"). Then the function select_optimal() of your initialized model object can be used to choose the optimal method. User need to provide three options:

  • molecule (mlatom.data.molecule): the input molecule

  • nCPUs (int): the number of CPUs used.

  • time_budget (str): the expected time used. s, m, h and d can be recognized, e.g. 3m.

A simple example to perform single-point calculation is provided:

import mlatom as ml

mol = ml.data.molecule.from_xyz_string('''5

C         0.0000000000        0.0000000000        0.0000000000
H         1.0870000000        0.0000000000        0.0000000000
H        -0.3623333220       -1.0248334322       -0.0000000000
H        -0.3623333220        0.5124167161       -0.8875317869
H        -0.3623333220        0.5124167161        0.8875317869
''')

uaiqm_optimal = ml.models.uaiqm(method='uaiqm_optimal', verbose=True)
# verbose = True in the above line requests to print the information about the model
uaiqm_optimal.select_optimal(
    molecule=mol,
    nCPUs=1,
    time_budget='1s'
)
uaiqm_optimal.predict(molecule=mol, calculate_energy=True)
print(mol.energy)

备注

If time_budget is set to 0s, selection will only be performed among UAIQM methods without baseline.

Manual model choice

For input file, similar to other methods defined in MLatom, user just need to request the keyword for the specific UAIQM model in the first line. uversion can be used to specify the version for each UAIQM method. A simple example for single-point calculations would be:

uaiqm_gfn2xtbstar@cc
uversion=20240106 # optional, by default the latest version
xyzfile='
5

C         0.0000000000        0.0000000000        0.0000000000
H         1.0870000000        0.0000000000        0.0000000000
H        -0.3623333220       -1.0248334322       -0.0000000000
H        -0.3623333220        0.5124167161       -0.8875317869
H        -0.3623333220        0.5124167161        0.8875317869

'
yestfile=enest.dat

With Python API, user just need to specify the method name and version of the method with ml.models.methods module:

import mlatom as ml

uaiqm = ml.models.methods(method='uaiqm_gfn2xtbstar@cc', version='newest') # latest version
# uaiqm = ml.models.methods(method='uaiqm_gfn2xtbstar@cc') # latest version
# uaiqm = ml.models.methods(method='uaiqm_gfn2xtbstar@cc', version='20240106') # user specified version

Setting number of threads

If user want to set threads used for baseline, for example DFT, baseline_kwargs can be used as:

uaiqm = ml.models.methods(method='uaiqm_wb97xdef2tzvpp@cc', version='newest', baseline_kwargs={'nthreads':18})

By default all the CPUs available will be used.

Handling uncertain warnings

In UAIQM methods, we use calibrated uncertainty provided by ML models to judge whether the calculations are reliable for the given the chemical system.

If the uncertainty exceeds the threshold, the calculation will give the warning WARNING: Uncertainty is too high for selected UAIQM method. Do not panick! This warning does not mean the calculation is bad – it is just not satisfying our strict conditions which typically ensure 1 kcal/mol error in thermochemical properties. Check the standard deviation value, if it is, e.g., +/-2.4 kcal/mol, it might be well acceptable for your simulations (common DFT methods have even larger error bars!).

In the meantime, we will improve the UAIQM methods for such systems so in the future your system will be calculated with lower uncertainty and higher accuracy.

We provide uwarning in input file

uaiqm
uwarning=False
xyzfile='2

H         0.0000000000        0.0000000000        0.0000000000
H         0.7414000000        0.0000000000        0.0000000000
'
yestfile=enest.dat

and warning option in python API

uaiqm = ml.models.methods(method='uaiqm_gfn2xtbstar@cc', warning=False)

to control these warnings (expecially for tasks like geometry optimization and molecular dynamics where multiple calculations will be performed at one time and the warnings may be crowded into the output). Currently, the uncertain warnings are by default switched on.

Application examples

Single-point calculations

For detailed information on how to use MLatom to perform single-point calculation, please refer to our tutorial.

In MLatom input file, after defining the UAIQM method, the XYZ geometries of molecules need to be provided with xyzfile keyword, which can be either a .xyz file or literal strings. Energy, gradients and hessian can be obtained by using yestfile, ygradxyzestfile and hessianestfile keywords:

uaiqm_gfn2xtbstar@cc
xyzfile=ch4.xyz
yestfile=enest.dat
ygradxyzestfile=grad.dat
hessianestfile=hess.dat

where ch4.xyz contains:

5

C         0.0000000000        0.0000000000        0.0000000000
H         1.0870000000        0.0000000000        0.0000000000
H        -0.3623333220       -1.0248334322       -0.0000000000
H        -0.3623333220        0.5124167161       -0.8875317869
H        -0.3623333220        0.5124167161        0.8875317869

In MLatom output file, energy for each component will be provided as:

==============================================================================

Properties of molecule 1

Standard deviation of ML contribution    :      0.00009751 Hartree         0.06119 kcal/mol
Baseline contribution                    :     -4.17449690 Hartree
NN contribution                          :    -36.29026149 Hartree
D4 contribution                          :     -0.00010193 Hartree
Total energy                             :    -40.46486033 Hartree

==============================================================================

To use Python API to perform single-point calculations, user can use mlatom.data.molecule or mlatom.data.molecular_database to load molecule(s) and predict() function to get energies, gradients and hessians, e.g.:

import mlatom as ml

mol = ml.data.molecule.from_xyz_file('ch4.xyz')

uaiqm = ml.models.methods(method='uaiqm_gfn2xtbstar@cc')

uaiqm.predict(
    molecule = mol,
    calculate_energy = True,
    calculate_energy_gradients = True,
    calculate_hessian = True
)

print(f'Standard deviation of ML contribution: {mol.energy_standard_deviation:.6f} Hartree ' \
    + f'{mol.energy_standard_deviation * ml.constants.Hartree2kcalpermol:.6f} kcal/mol')
print(f'Baseline contribution: {mol.baseline_energy:.6f} Hartree')
print(f'NN contribution: {mol.MLs_energy:.6f} Hartree')
print(f'D4 contribution: {mol.dispersion_energy:.6f} Hartree')
print(f'Total energy: {mol.energy:.6f} Hartree')

print('\nGradients for molecule:')
print(mol.get_energy_gradients())

print('\nHessian for molecule:')
print(mol.hessian)

Geometry optimization

For detailed information on how to use MLatom to perform geometry optimization, please refer to our tutorial.

In input file, keyword geomopt is required after defining the UAIQM methods, i.e.

uaiqm_gfn2xtbstar@cc
geomopt
xyzfile='5

C         0.0000000000        0.0000000000        0.0000000000
H         1.0870000000        0.0000000000        0.0000000000
H        -0.3623333220       -1.0248334322       -0.0000000000
H        -0.3623333220        0.5124167161       -0.8875317869
H        -0.3623333220        0.5124167161        0.8875317869
'

User can use optxyz to specify the file with optimized geometry (by default it is stored in optgeoms.xyz). MLatom also provides options to control how much information is saved with :

  • printmin will not print information about every iteration.

  • printall will print detailed information at each iteration.

  • dumpopttrajs=False will not dump any optimization trajectories.

For Python API, MLatom uses mlatom.optimize_geometry to perfrom geometry optimization, e.g.:

import mlatom as ml

# Get the initial guess for the molecules to optimize
initmol = ml.data.molecule.from_xyz_string('''5

C         0.0000000000        0.0000000000        0.0000000000
H         1.0870000000        0.0000000000        0.0000000000
H        -0.3623333220       -1.0248334322       -0.0000000000
H        -0.3623333220        0.5124167161       -0.8875317869
H        -0.3623333220        0.5124167161        0.8875317869
''')

# define UAIQM method
uaiqm = ml.models.methods(method='uaiqm_gfn2xtbstar@cc')

# Optimize the geometry with the choosen optimizer:
geomopt = ml.optimize_geometry(model=uaiqm, initial_molecule=initmol, program='geometric')

# Get the final geometry
final_mol = geomopt.optimized_molecule
# and its XYZ coordinates
final_mol.xyz_coordinates

# save the final geometry
final_mol.write_file_with_xyz_coordinates(filename='final.xyz')

Available optimizers are gaussian, ase and geometric. User can request one of them with optprog in input file and program in Python API.

Frequencies and thermochemistry

For detailed information on how to use MLatom to perform frequency calculation, please refer to our tutorial.

In input file, keyword freq is required after defining the UAIQM methods, i.e.

uaiqm_gfn2xtbstar@cc
freq
xyzfile=optgeoms.xyz

where we use the optimized geometry from previous step:

5

C             0.0000000045659          -0.0000000007924           0.0000000006329
H             1.0871538632866          -0.0000000003649           0.0000000011025
H            -0.3623846148156          -1.0249784859702           0.0000000000380
H            -0.3623846095164           0.5124892422251          -0.8876574044417
H            -0.3623846107429           0.5124892415915           0.8876574054188

After frequency calculation, vibration analysis and thermochemistry for the molecule are provided in the output file as:

==============================================================================
                  Vibration analysis for molecule      1
==============================================================================
Multiplicity: 1
Rotational symmetry number: 1
This is a nonlinear molecule
Mode     Frequencies     Reduced masses     Force Constants
            (cm^-1)            (AMU)           (mDyne/A)
    1       1350.8213          1.1812             1.2699
    2       1350.8617          1.1812             1.2700
    3       1350.9106          1.1812             1.2701
    4       1569.9022          1.0080             1.4637
    5       1569.9122          1.0080             1.4637
    6       3054.4203          1.0080             5.5407
    7       3156.5711          1.0999             6.4573
    8       3156.6051          1.0999             6.4574
    9       3156.7927          1.0999             6.4582
==============================================================================
                    Thermochemistry for molecule      1
==============================================================================
Standard deviation of ML contribution    :      0.00009751 Hartree         0.06119 kcal/mol
Baseline contribution                    :     -4.17449301 Hartree
NN contribution                          :    -36.29026544 Hartree
D4 contribution                          :     -0.00010194 Hartree
Total energy                             :    -40.46486038 Hartree

ZPE-exclusive internal energy at      0 K:       -40.46486 Hartree
Zero-point vibrational energy            :         0.04492 Hartree
Internal energy                  at   0 K:       -40.41994 Hartree
Enthalpy                         at 298 K:       -40.41613 Hartree
Gibbs free energy                at 298 K:       -40.43960 Hartree

Atomization enthalpy             at   0 K:         0.76880 Hartree       482.43218 kcal/mol
ZPE-exclusive atomization energy at   0 K:         0.81372 Hartree       510.61875 kcal/mol
Heat of formation                at 298 K:        -0.17234 Hartree      -108.14800 kcal/mol

==============================================================================

For Python API, MLatom uses mlatom.freq to perfrom frequency calculation and with mlatom.thermochemistry additional themochemical analysis is provided. A simple example is shown below for workflow of optimizing geometry and calculating frequency:

import mlatom as ml

# Get the initial guess for the molecules to optimize
initmol = ml.data.molecule.from_xyz_string('''5

C         0.0000000000        0.0000000000        0.0000000000
H         1.0870000000        0.0000000000        0.0000000000
H        -0.3623333220       -1.0248334322       -0.0000000000
H        -0.3623333220        0.5124167161       -0.8875317869
H        -0.3623333220        0.5124167161        0.8875317869
''')

# define UAIQM method
uaiqm = ml.models.methods(method='uaiqm_gfn2xtbstar@cc')

# Optimize the geometry with the choosen optimizer:
geomopt = ml.optimize_geometry(model=uaiqm, initial_molecule=initmol, program='geometric')

# Get the final geometry
final_mol = geomopt.optimized_molecule

# Do vibration analysis and thermochemistry calculation
freq = ml.thermochemistry(model=uaiqm, molecule=final_mol, program='pyscf')
# or vibration analysis only
# freq = ml.freq(model=uaiqm, molecule=final_mol, program='pyscf')

# Save the molecule with vibration analysis and thermochemistry results
final_mol.dump(filename='final_mol.json',format='json')

# Check vibration analysis
print("Mode     Frequencies     Reduced masses     Force Constants")
print("           (cm^-1)            (AMU)           (mDyne/A)")
for ii in range(len(final_mol.frequencies)):
    print("%d   %13.4f   %13.4f   %13.4f"%(ii,final_mol.frequencies[ii],final_mol.reduced_masses[ii],final_mol.force_constants[ii]))

# Check thermochemistry results
print(f"Zero-point vibrational energy: {final_mol.ZPE} Hartree")
print(f"Enthalpy at 298 K: {final_mol.H} Hartree")
print(f"Gibbs Free energy at 298 K: {final_mol.G} Hartree")
print(f"Heat of formation at 298 K: {final_mol.DeltaHf298} Hartree")

Available programs to perform frequency calculations are gaussian, pyscf and ase. User can request one of them with freqprog in input file and program in Python API.

IR spectra

MLatom provides easy-to-use options to get infrared spectra. For detailed information on how to use MLatom to obtain infrared spectra, please refer to our ir tutorial.

Simulating infrared spectra with UAIQM methods using input file in MLatom is ultra easy with only 3 lines:

ir
uaiqm_wb97x631gp@cc
xyzfile=opt.xyz

where the opt.xyz is the ethanol optimized by uaiqm_wb97x631gp@cc as:

9

C             1.2141461144075          -0.2237522351565           0.0000009660331
H             1.2725810451795          -0.8571489137580          -0.8839209229985
H             1.2725955610560          -0.8571196861893           0.8839423252131
H             2.0641316742868           0.4586264688194          -0.0000176008701
C            -0.0820255073362           0.5506969112630          -0.0000006009490
H            -0.1394716683438           1.1910011723471           0.8856982674255
H            -0.1394676608187           1.1909953759585          -0.8857037188954
O            -1.1431943032587          -0.3953014469416          -0.0000014007109
H            -1.9775381677168           0.0743891017157           0.0000106653069

Vibrational analysis and IR intensities can be found in MLatom output files:

==============================================================================
                  Vibration analysis for molecule      1
==============================================================================
Multiplicity: 1
This is a nonlinear molecule
Mode     Frequencies     Reduced masses     Force Constants       IR intensities
            (cm^-1)            (AMU)           (mDyne/A)              (km/mol)
    1        241.0374          1.1507             0.0394                86.1148
    2        297.4762          1.0709             0.0558                54.1970
    3        418.2334          2.5803             0.2659                12.4199
    4        810.5925          1.0759             0.4165                 0.0530
    5        910.3415          2.1135             1.0319                12.0631
    6       1048.6773          1.8779             1.2167                48.5102
    7       1125.4218          2.7007             2.0154                37.0761
    8       1193.0919          1.5109             1.2672                 5.4162
    9       1274.9990          1.2567             1.2037                83.6804
    10       1305.5061          1.1150             1.1196                 0.0292
    11       1404.9278          1.2383             1.4401                 2.1079
    12       1454.1580          1.4707             1.8323                16.1926
    13       1493.5120          1.0405             1.3674                 5.3892
    14       1508.6873          1.0534             1.4126                 3.9672
    15       1539.9937          1.0936             1.5280                 2.0331
    16       2996.6657          1.0554             5.5840                65.1341
    17       3032.2203          1.1085             6.0050                66.4608
    18       3037.2688          1.0350             5.6253                14.7477
    19       3120.1171          1.1012             6.3160                27.1681
    20       3126.3285          1.1032             6.3532                28.7563
    21       3844.2694          1.0659             9.2813                22.8496
==============================================================================
                    Thermochemistry for molecule      1
==============================================================================
Selected UAIQM method: uaiqm_wb97x631gp@cc
Selected version: latest

Standard deviation of ML contribution    :      0.00014563 Hartree         0.09139 kcal/mol
Baseline contribution                    :   -154.98764057 Hartree
NN contribution                          :      0.09856558 Hartree
D4 contribution                          :     -0.00044829 Hartree
Total energy                             :   -154.88952328 Hartree

ZPE-exclusive internal energy at      0 K:      -154.88952 Hartree
Zero-point vibrational energy            :         0.08015 Hartree
Internal energy                  at   0 K:      -154.80937 Hartree
Enthalpy                         at 298 K:      -154.80413 Hartree
Gibbs free energy                at 298 K:      -154.83475 Hartree

Atomization enthalpy             at   0 K:         1.25151 Hartree       785.33412 kcal/mol
ZPE-exclusive atomization energy at   0 K:         1.33166 Hartree       835.63152 kcal/mol
Heat of formation                at 298 K:        -0.12976 Hartree       -81.42550 kcal/mol

==============================================================================

With Python, user just need to set ir=True for frequency calculation, i.e.:

import mlatom as ml

# load optimized molecule
optmol = ml.data.molecule.from_xyz_file('opt.xyz')

# define uaiqm method
uaiqm = ml.models.methods(method='uaiqm_wb97x631gp@cc')

# perfrom frequency calculation
freq = ml.freq(model=uaiqm, molecule=optmol, ir=True)

# get intensities
print(optmol.infrared_intensities)

and the intensities will be stored in infrared_intensities of molecule object.

备注

Currently, ir intensities can only be obtained with DFT based UAIQM methods, i.e. uaiqm_wb97x631gp@cc, and uaiqm_wb97xdef2tzvpp@cc

Reaction energies for Diels–Alder Reaction

We prepared DARC dataset from GMTKN55 in json format. The file contains 14 Diels–Alder reactions, each of which will take several CPU hours for popular hybrid and double-hybrid DFT to approach chemical accuracy (1 kcal/mol). Here, we will select the cheap UAIQM model by limiting the time budget to 0.1 s. The final results will be written to reaction_summary and molecule_summary where the prediction of reaction energies, UAIQM method used for each molecule and their uncertainty are stored. If verbose=True, then information for each selection step will be reported.

import mlatom as ml

# load reaction dataset
darc = ml.data.reactions_database()
darc.load(f'DARC.json', format='json')

darc_uaiqm = ml.data.reactions_database()
for reaction in darc.reactions:
    for mol in reaction.molecules:
        # initialize uaiqm optimal method
        uaiqm_optimal = ml.models.uaiqm(method='uaiqm_optimal', verbose=False) # set verbose to True to get the report for each selection step
        uaiqm_optimal.select_optimal(
            molecule=mol,
            nCPUs=1,
            time_budget='1s'
        )
        uaiqm_optimal.predict(molecule=mol, calculate_energy=True)
        mol.uaiqm_method = uaiqm_optimal.method
    reaction.absolute_energy()
    darc_uaiqm.reactions.append(reaction)

# write darc_uaiqm to MLatom format json file
darc_uaiqm.dump(f'DARC_with_UAIQM_methods.json', format='json')

# write results to reaction_summary and molecule_summary
molecule_summary = open(f'molecule_summary', 'w')
molecule_summary.write('mol\tpred\tuaiqm_method\tUQ\n')
reaction_summary = open(f'reaction_summary', 'w')
reaction_summary.write('reaction\tref\tpred\n')

for reaction in darc_uaiqm.reactions:
    print(reaction.chemical_label)
    reaction_summary.write(f'{reaction.chemical_label}\t{reaction.ref}\t{reaction.energy*ml.constants.Hartree2kcalpermol}\n')
    for mol in reaction.molecules:
        molecule_summary.write(f'{mol.chemical_label}\t{mol.energy*ml.constants.Hartree2kcalpermol}\t{mol.uaiqm_method}\t{mol.energy_standard_deviation*ml.constants.Hartree2kcalpermol}\n')
reaction_summary.close()
molecule_summary.close()

# get MAE for DARC datasets
import pandas as pd
darc_summary = pd.read_csv(f'reaction_summary', sep='\t')
mae = abs(darc_summary['pred']-darc_summary['ref']).mean()
print(f'MAE for DARC datasets: {mae} kcal/mol\n')

Quasiclassical trajectories analysis on the bifurcating pericyclic reaction

In this section, we will reproduce the quasiclassical trajectories for bifurcating pericyclic reaction reported in JACS (2017) 139, 8251, where the human experts manually chosen the B3LYP-D3/6-31G* level of theory and got the distribution of the products with the resulting 117 reactive trajectories. With the UAIQM models, we can quickly shoot 1000 trajectories and get hundreds of reactive ones, while the energy profile is more accurate than B3LYP which is known for low reliability on energy prediction.

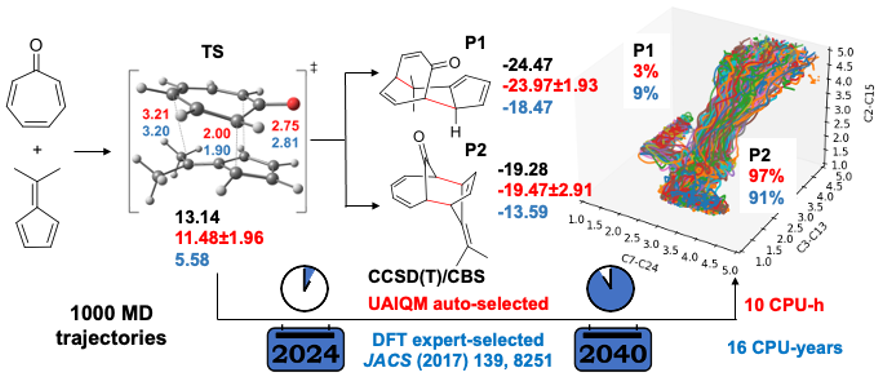
_images/qct.png

Below we provide instructions on the procedure to propagate one trajectory with our UAIQM models. Time budget is reduced to 0.1 s for UAIQM method. The same setting for quasi-classical MD will be used as that in the original paper, i.e. 500 fs long trajectory with 1 fs time step starting from region near ambimodal transition state. Initial transition state file can be downloaded: TS1.xyz (We also provide it explicitly in the script).

备注

We provide the Jupyter notebook ambimodal.ipynb for this example, which we also placed into jupyter_examples/uaiqm folder on the XACS cloud, where you can run it after launching the Jupyter lab. To submit a job with on more CPU nodes for hundreds of trajectories, please run sbatch ambimodal.sh provided under jupyter_examples/uaiqm/slurm folder.

ambimodal

Data policy

The users can perform the UAIQM simulations with the following data policies:

  • fully open access (the data and models might be made openly available in the future). Default option. Basic simulations are free of charge according to the default policy of the XACS cloud computing.

  • data-protected calculations (data will not be shared with anyone but models trained on them might be made open access). Needs to be requested by contacting xacs@xmu.edu.cn.

  • fully private (the data will not be shared with anyone and the models will not be improved). Needs to be requested by contacting xacs@xmu.edu.cn.

备注

Above data polices only apply to UAIQM calculations. Other calculations are fully private on the XACS cloud, see the privacy policy.

Any questions or suggestions?

If you have further questions, criticism, and suggestions, we would be happy to receive them in English or Chinese via email, Slack (preferred), or WeChat (please send an email to request to add you to the XACS user support group).