2. ML for PES

2.1. Slides

Slides:

2.2. Machine learning potentials

You have already used the KREG models. The operating principle of these models is the same: for a given geometry, they predict energies. Hence, such models are called machine learning (interatomic) potentials (in literature abbreviated as both MLP or MLIP), as they represent potential energy surfaces (PES) of molecules (function of energy \(E\) with respect to nuclear coordinates \(\mathbf{R}\) in the Born–Oppenheimer approximation, see literature on quantum chemistry):

\[E = f(\mathbf{R}).\]

As we have already seen, QM methods provide the first-principles way to calculate this energy, but they are slow and, hence, there is a huge insentive to use ML to learn from the data the dependence of energy on nuclear coordinates. ML functions are much faster to evaluate because they are relatively simple compared to the numerically intensive QM algorithms.

There is the whole zoo of MLPs with typical representatives shown below (the potentials in bold are supported by MLatom):

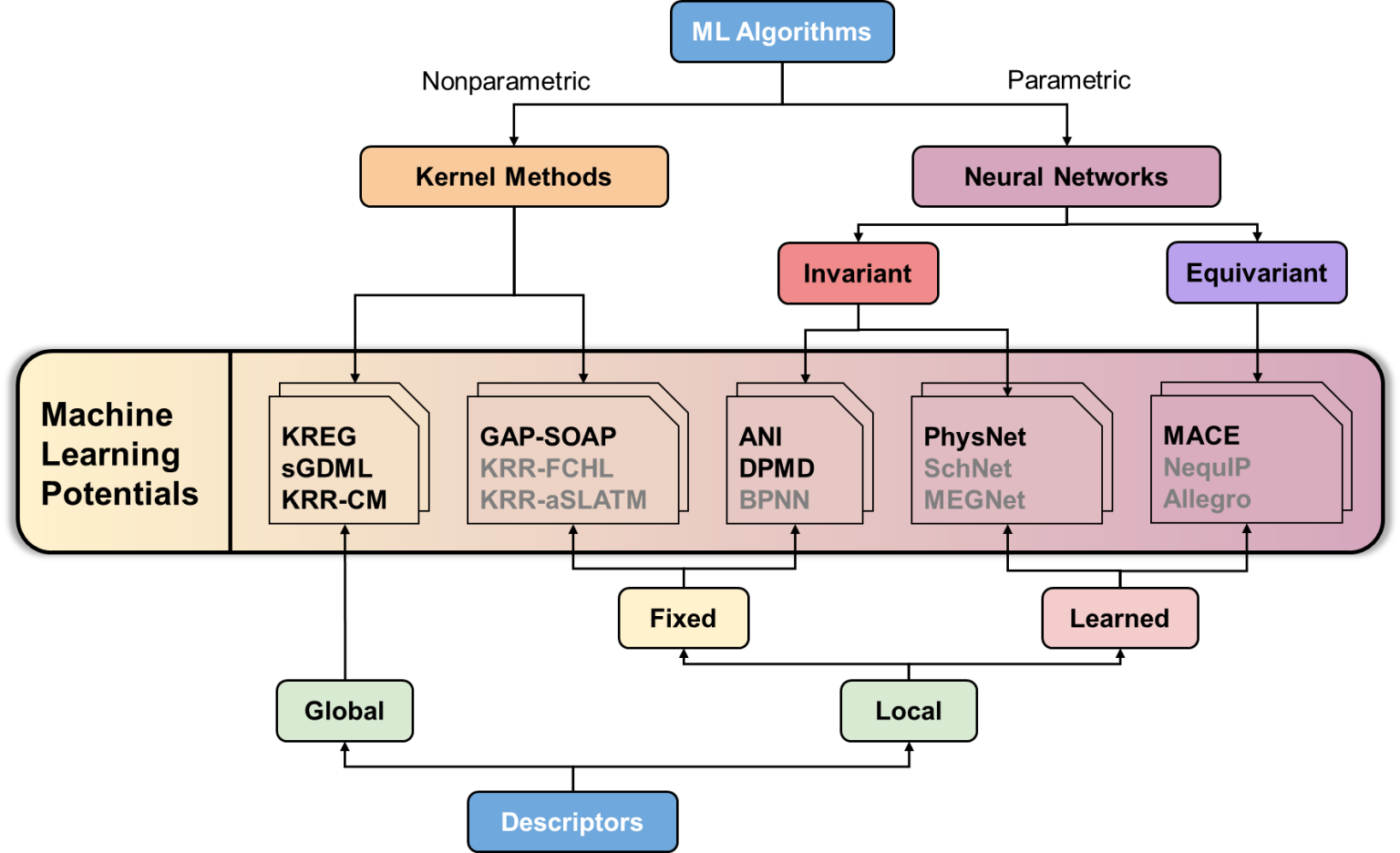
If this zoo seems intimidating – it is. But do not worry, we will start with simple hands-on examples to get the feeling about different MLPs and explain along the way what we should pay attention to, when choosing MLPs.

Let’s first get a taste of different flavors of MLPs by extending our first example of ML calculations. There we trained the KREG model on the data for the H₂ molecule and used this MLP to optimize its geometry. As usual, for training MLPs we need the corresponding data – energies and coordinates. In the following task, we will try another model of a completely different type and will see what happens:

Example PES1.

Train the ANI-type MLP for the H₂ molecule (see instructions below) and obtain the bond length with this model.

Questions:

How much time did it take to train the model?
What are the training and validation errors?
What is the bond length of H₂ obtained with your model?
How do these results compare to the KREG model you used in previous task?

The MLatom@XACS input file with expanation in comments:

createMLmodel               # Specify the task for MLatom
MLmodelType=ANI             # Specify the model type
MLmodelOut=energies_ani.pt  # Save model in energies_ani.pt
XYZfile=h2.xyz              # File with XYZ geometries
Yfile=E_FCI_451.dat         # The file with FCI energies but can be any other property
ani.max_epochs=1000         # Only train 1000 epochs

For geometry optimizations, you need to specify the model type and the model file as with KREG model:

geomopt                     # Request geometry optimization
MLmodelType=ANI             # of the KREG type
MLmodelIn=energies_ani.pt   # in energies_ani.pt file
XYZfile=h2_init.xyz         # The file with initial guess
optXYZ=eq_ANI.xyz           # optimized geometry output

You need two auxiliary files with data:

E_FCI_451.dat – energies in Hartree.
h2.xyz – geometries.

After you run these simulations, it is useful to compare the results with other people around you. Or you can run them several times…

What you will notice is that:

ANI is definetely much slower than the KREG training,
ANI results are all over the place, while KREG always produces the same result.

To understand why, you need to understand the underlying differences between the ML algorithms.

2.3. Testing ML models

Once you trained the model, you should always test how well it performs. Let’s first see what can go wrong when you train a model and leave it unchecked:

Example PES2.

Train the KREG model for the H₂ molecule with the settings provided below. With this model, calculate energies for the potential energy curve of H₂ (see instructions below).

Questions:

What is the training error (RMSE) of the model?
Does the potential energy curve (energy as a function of the bond length) look reasonable?

Input file for training KREG model:

createMLmodel           # Specify the task for MLatom
MLmodelType=KREG        # Specify the model type
MLmodelOut=kreg.unf # Save model in kreg.unf
XYZfile=h2.xyz          # File with XYZ geometries
Yfile=E_FCI_451.dat     # The file with FCI energies
Ntrain=50
sigma=0.01
lambda=0.0

Input file for predicting energies with the ML model:

useMLmodel           # Specify the task for MLatom
MLmodelType=KREG        # Specify the model type
MLmodelIn=kreg.unf # Save model in kreg.unf
XYZfile=h2.xyz          # File with XYZ geometries
YestFile=E_FCI_451_kreg_est.dat     # The file with FCI energies

The predicted energies will be saved in E_FCI_451_kreg_est.dat. You can plot them in Excel as a function of the interatomic distance provided in the file R_451.dat and compare to the reference energies with full CI in the file E_FCI_451.dat.

Note

You need two auxiliary files with data (energies in E_FCI_451.dat and geometries in h2.xyz).

As you see from above task, the modern ML models are so flexible that they can easily memorize the training data (the severa case of overfitting) while our goal is to make good predictions for points outside the training set. Hence, the standard practice is to evaluate the error of the ML models on an independent test set. Let’s do it in the next task.

Example PES3.

Estimate the accuracy of the KREG model for the H₂ molecule for the test set.

Questions:

What is the test error (RMSE) of the model?
How does it compare to the training error?
Does the model test error reflect its performance for the potential energy curve in previous task?

Input file:

estAccMLmodel           # Specify the task for MLatom
MLmodelType=KREG        # Specify the model type
XYZfile=h2.xyz          # File with XYZ geometries
Yfile=E_FCI_451.dat     # The file with FCI energies
Ntrain=50
sigma=0.01
lambda=0.0

Use the auxiliary files from the previous tasks.

All these are just initial tests. The ultimate test is the performance in the required application!

2.4. Choosing ML model settings to make it work

We saw that it is easy to overfit the model. However, we do not want to underfit it either, i.e., to obtain a bad model that does not even learn the known data. How well the model fits on the known and generalizes to the unknown data strongly depends on the settings of the model. These settings, known as hyperparameters, are not model parameters which are optimized during training but they influence the training outcome.

If we think about NN, then such hyperparameters can be the number of layers, number of neurons in each layer, the choice of activation function, the batch size and learning rate. In case of KRR, there might be hyperparameters entering the kernel function (e.g., the Gaussian width) and all of them have a regularization hyperparameter that imposes penalty on the magnitude of regression coefficients so that the model’s variance around the known data is not too large – the larger regularization usually leads to a more generalizable model but with a higher fitting error.

In general, there is usually a sweet spot in the choice of hyperparameters, known as bias-variance tradeoff. Practically, it is done by splitting the training set into the sub-training (often, confusingly called training set too) and the validation set. The hyperparameters are optimized so that the error on the validation set is the lowest. In case of the NNs, the model is often trained until the error on the validation set does not decrease for some number of epochs known as patience; when this point is reached the training is stopped and this approach is called early stopping.

Note that since the validation set is indirectly used to obtain a better model, it cannot be used to judge the generalization error which must be evaluated on the independent test set. Luckily, many of the packages, MLatom included, provide automatic routines for the choice of hyperparameters, see the next exercise.

Example PES4.

Estimate the accuracy of the KREG model for the H₂ molecule for the test set.

Questions:

What are the training, validation, and test errors (RMSE) of the model?
How does the potential energy curve now looks like? (Adapt input file from the previous task)

Input file:

estAccMLmodel           # Specify the task for MLatom
MLmodelType=KREG        # Specify the model type
MLmodelOut=kreg_opt.unf # Save model in kreg_opt.unf
XYZfile=h2.xyz          # File with XYZ geometries
Yfile=E_FCI_451.dat     # The file with FCI energies
Ntrain=50
sigma=opt
lgSigmaL=-4             # Lower bound of log2(sigma)
lambda=opt

Use the auxiliary files from the previous tasks.

As for choosing the best MLP, it is not an easy question as it depends on the task at hand. Practically speaking, NNs tend to be used more and among them options like ANI provide good balance between speed (training and evaluation) and accuracy but if you can afford equivariant networks such as MACE, you should try. MACE is definetely slower but there is a growing evidence that it becomes an algorithm of choice when accurate and robust results are needed.

2.5. Importance of including forces in training MLPs

Last but not least, when training MLPs, you must always utilize derivative information if available. The first-order derivative of energy with respect to nuclear coordinates is energy gradient or negative force and it is available in many but not all QM methods. When trained on both energies and forces, the models have much higher accuracy and even though the training is slower, it is worth doing. MLatom provides an easy way to train all of the supported MLPs on both energies and forces.

You can check how the results improve when you train the model with energy gradients in addition to energies.

Example PES5.

Check how the test error changes when you include energy gradients during the training of an MLP. Note also, how much time you need to train with and without energy gradients.

You might need to repeat calculations couple of times and might want to change the number of training points.

Input file:

estAccMLmodel           # Specify the task for MLatom
MLmodelType=KREG        # Specify the model type
MLmodelOut=kreg_grad.unf # Save model in kreg_opt.unf
XYZfile=H2.xyz           # file with geometies
Yfile=H2_HF.en           # file with energies
YgradXYZfile=H2_HF.grad  # file with energy gradients
Ntrain=20
Nsubtrain=0.9           # request 90% of the training points to be used for validation
sigma=opt
lgSigmaL=-4             # Lower bound of log2(sigma)
lambda=opt
lgLambdaL=-8             # Lower bound of log2(lambda)

The provided data is generated at HF/STO-3G and you can download it as a zipped folder. It contains:

H2.xyz - xyz coordinates
H2_HF.en - energies at HF/STO-3G
H2_HF.grad - energy gradients at HF/STO-3G

This example reflects the well-recognized advice that you must include forces during training when they are available!

2.6. Splitting

You have might been disappointed that the model trained in the previous task sometimes was still not good enough. One of the reasons is that the validation set is quite large in default settings in MLatom (20% of the training set). While it is a safe option for many applications, practice shows that 10% is sufficient (i.e., 9:1 splitting of the training set). Some people may argue that cross-validation is required and this is also supported in MLatom, but again, practice shows that it is overkill. Hence in the next homework you have a chance to get more robust model by playing with different splittings.

Example PES6.

Estimate the accuracy of the KREG model for the H₂ molecule for the test set by using the 9:1 splitting of the training set for hyperparameter optimization, i.e., using 10 of the training data for the validation set. To see how stability of the results change compared to 8:2 splitting, you can run this experiment several times and compare the test error and the potential energy curves.

Input file:

estAccMLmodel           # Specify the task for MLatom
MLmodelType=KREG        # Specify the model type
MLmodelOut=kreg_opt.unf # Save model in kreg_opt.unf
XYZfile=h2.xyz          # File with XYZ geometries
Yfile=E_FCI_451.dat     # The file with FCI energies
Ntrain=50
Nsubtrain=0.9           # request 90% of the training points to be used for validation
sigma=opt
lgSigmaL=-4             # Lower bound of log2(sigma)
lambda=opt

Use the auxiliary files from the previous tasks.

The results must become substantially more stable. To be honest, 9:1 splitting is sufficient and some people even go to extremes and use something like 50 out of 1k training points for validation. MLatom’s default setting of 8:2 splitting is probably too conservative and might be changed in the future to 9:1 as that is what we now mostly using in practice. You need to check yourself what kind of splitting works best for your problem.

2.7. Learning curves

Example PES7.

Investigate how the performance of the KREG model changes for different number of the training points. Modify the Ntrain parameter in the input file below. Particularly for smaller number of training points, there is a wide spread of results, so they should be repeated more times.

Input file:

estAccMLmodel           # Specify the task for MLatom
MLmodelType=KREG        # Specify the model type
MLmodelOut=kreg_opt.unf # Save model in kreg_opt.unf
XYZfile=h2.xyz          # File with XYZ geometries
Yfile=E_FCI_451.dat     # The file with FCI energies
Ntrain=50
Nsubtrain=0.9           # request 90% of the training points to be used for validation
sigma=opt
lgSigmaL=-4             # Lower bound of log2(sigma)
lambda=opt

MLatom has an automatic way of generating the dependence of the test error on the size of the training set. The input file can look like:

learningCurve
lcNtrains=10,20,50,100,200,300
lcNrepeats=5,4,3,2,1,1
Ntest=100
MLmodelType=KREG        # Specify the model type
MLmodelOut=kreg_opt.unf # Save model in kreg_opt.unf
XYZfile=h2.xyz          # File with XYZ geometries
Yfile=E_FCI_451.dat     # The file with FCI energies
Nsubtrain=0.9
sigma=opt
lgSigmaL=-4             # Lower bound of log2(sigma)
lambda=opt

The results of these calculations will be saved in learningCurve/mlatomf_KREG_en folder, where the file lcy.csv collates the information which you can, e.g., plot in Excel.

Use the auxiliary files from the previous tasks.

This example is showing you how to perform the type of analysis that we have done some time ago (in 2020-2021) which became one of the highly cited articles in a prestigeous Chemical Science journal:

Note, however, that the field is moving forward fast and conclusions we drew in 2021 do not reflect all the developments afterwards. Particularly, I would really recommend to have a look at the equivariant NNs like MACE! Luckily, with MLatom you can easily perform the same type of analysis for the new MLPs to draw your own conclusions.