3. Computing of F₂

3.1. Introduction

F₂ is a typical diatimic molecule which is simple enough for the users as a starting point. There is only 1 chemical bonding in the molecule. The 3 structures of the bonding is shown below.

Structures of F₂ molecule

Here S1 denotes the covalent structure in which two active electrons are shared between both F atoms while S2 and S3 denote 2 quivalent ionic structures in which two active eletrons doubly occupy orbital on certain F atom.

In this exercise, we will try to proceed computations for the bond dissociation energy (BDE) and resnance energy (RE) of F2. This takes computations at stationary point and dissociation limit with various sets of VB structures.

In this example, we will also investigate the nature of the F-F bonding, which is not the conventional covalent or ionic bond, but is charge-shift bond.

Electron-pair bonding is a central chemical paradigm to describe and interpret the interaction between atoms in a molecule. The concepts of covalent and ionic bonds can be dated back to the ingenious hypothesis of Lewis in 1916, and are still widely accepted and used nowadays. The covalent bonding comes from the electron spin-pairing of adjacent atoms and thus strongly stabilizes the molecule, while the ionic bonding comes from the electrostatic interaction of two fragments with opposite charges. Typical covalent bonds are usually found between H, B, C, N, O atoms, while typical ionic bonds are formed with one alkali or alkaline earth metal atom and one halogen atom. However, despite great successes of traditional electron-pair bonding in explaining molecular stability and chemical reaction mechanisms, the chemical bonding even in some simple molecules, F₂ for instance, cannot be unambiguously classified into covalent or ionic.

The following figure shows the dissociation curves of the total wave function and covalent structure for H₂ and F₂ molecules. For H₂, the potential energy curve (PEC) of covalent structure is a little higher than that of the total wave function, but the topology of the both PECs is quite close. One thus concludes that the bonding in H₂ is dominated by the covalent interaction between the two H atoms. For F₂, however, the PEC of covalent structure is repulsive, and much higher than that of the total wave function, and the topology of the two PECs is totally different, i.e. the two F atoms tend to dissociate due to the covalent interaction. Since both the covalent and ionic interactions are non-bonding in F₂, the bond dissociation energy (BDE) of F₂, which is around 38.2 kcal/mol, is totally due to the resonance of the VB structures. Based on the above-mentioned novel bonding, Shaik and Hiberty et al. proposed a new type of chemical bond, charge-shift (CS) bond, in which the RE contributes over 50% to the BDE.

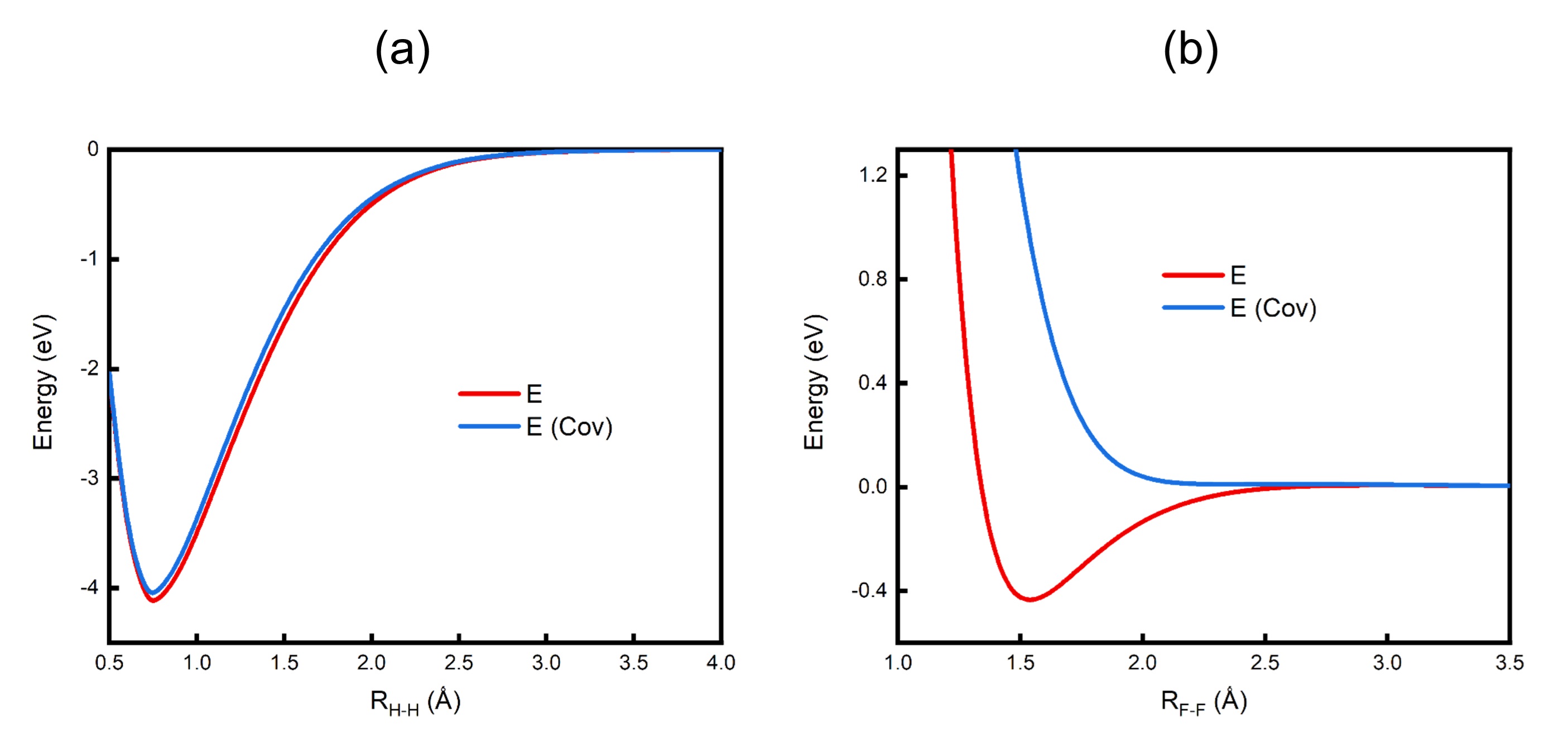
The dissociation curves of the total wave function and covalent structure for (a) H₂ and (b) F₂ molecules.

Note

This exercise just shows the users how to proceed a VBSCF computation for a specific molecule, what we can get from the output and how to analyze the results. The accurate computation of BDE of F₂ requires higher level computational methods with delocalized inactive \(\pi\) orbitals.

3.2. Computations with 3 Structures at Stationary Point

The computations are proceeded with F-F bond length 1.4 Angstrom, and the basis set is cc-pVDZ. For simplicity, F atoms are located in the Z axis.

3.2.1. Input File

Here shows the XMVB input file for all 3 structures at stationary point:

F2 VBSCF with 3 structures
$CTRL
STR=FULL NAO=2 NAE=2 IPRINT=3
ORBTYP=HAO FRGTYP=SAO
BASIS=CC-PVDZ
$END
$FRAG
1*6
SPZDXXDYYDZZ 1
SPZDXXDYYDZZ 2
PXDXZ 1
PXDXZ 2
PYDYZ 1
PYDYZ 2
$END
$ORB
1*10
1
2
1
2
3
4
5
6
1
2
$END
$GEO
F 0.0 0.0 0.0
F 0.0 0.0 1.4
$END

The global keywords listed in $CTRL section are explained below:

• STR=FULL XMVB generates all VB structures automatically according to a specific active space.

• IPRINT=3 XMVB will print most information.

• NAO=2 and NAE=2 Specify the active space with 2 active orbital and 2 active electrons respectively.

• ORBTYP=HAO and FRGTYP=SAO The VB orbitals are described with fragments.

• BASIS=CC-PVDZ The basis set is cc-pVDZ.

Note

The orbitals of a molecule can be devided into “inactive” and “active” parts. The inactive orbitals are always doubly occupied in all VB structures, while the occupation numbers of active orbitals can be 0, 1 or 2 in each VB structure.

$FRAG section describes the fragments used to construct VB orbitals. In this case, the first line 1*6 means that there are 6 fragments built and each fragment include only 1 atom. The details of fragments are described in the following lines. For example, SPZDXXDYYDZZ 1 means that the fragment includes s, p_z, d_xx, d_yy and d_zz basis functions on atom 1, which is the first F atom in this case.

$ORB section describes VB orbitals. The first line 1*10 means that there are 10 orbitals in this case, each consisting of only 1 fragment. Each line below describes one orbital. For example, the first orbital includes only fragment 1, meaning that this orbital locates on the first F atom and belongs to the \(\sigma\) space since the F-F lies on Z axis. Also, orbital 6 with fragment 4 shows that the orbital describes the \(\pi_x\) orbital on the first F atom.

$GEO section shows the geometry of F₂ molecule. Both Cartesian and internal coordinates are supported.

Note

Since NAO=2 is specified in $CTRL section, the last 2 orbitals in $ORB should be the active orbitals.

It is highly recommended that active orbitals are always palced after the inactive ones. This may make the input file more readable and less possible to get error.

3.2.2. Computational Results

In this case, 3 VB structures are generated with 1 covalent structure (0th ion structure) and 2 ionic structures (1th ion structures). These structures can be expaned into 4 determinants.

Number of   0th ion  structures  is:          1  from          1 to          1
Number of   0th ion determinants is:          2  from          1 to          2
Number of   1th ion  structures  is:          2  from          2 to          3
Number of   1th ion determinants is:          2  from          3 to          4
Total number of  structures  is:          3
Total number of determinants is:          4
                   .
                   .
                   .
Number of Structures:           3

The following structures are used in calculation:

      1 *****  1:8    9  10
      2 *****  1:8    9   9
      3 *****  1:8   10  10

The user may find from the output file that the VBSCF converged after 25 iterations and the final energy is -198.75115493 hartree.

                       VBSCF converged in    25 iterations

Total Energy:    -198.75115493

First Excited:   -197.880879

The coefficients and weights shows the importance of each structure. Following are the coefficients and weights of generated VB structures. Both coefficients and weights show that the covalent structure is the dominant one. So the F-F bond should be a covalent bond.

       ******  COEFFICIENTS OF STRUCTURES ******

1    -0.80579  ******  1:8    9  10
2    -0.21326  ******  1:8    9   9
3    -0.21326  ******  1:8   10  10
                  .
                  .
                  .
       ******  WEIGHTS OF STRUCTURES ******

1     0.77586  ******  1:8    9  10
2     0.11207  ******  1:8    9   9
3     0.11207  ******  1:8   10  10

Finally, the bond order value (0.773) in atomic population analysis shows that F-F bond should be a single bond.

          ******  BOND ORDER  ******

ATOM 1        ATOM 2           DIST     BOND ORDER

 1 F           2 F            1.400       0.773

3.3. Computations with 3 Structures at Dissociation Limit

3.3.1. Input File

The input file for such computation can be easily obtained by modifying the corresponding one at stationary point. As shown below, one just needs to modify the coordinate of the second F atom to change 1.4 to 10.0. This will increase the F-F bond distance to 10.0 Angstrom.

$GEO
F 0.0 0.0 0.0
F 0.0 0.0 10.0
$END

3.3.2. Computational Results

After SCF procedure, the user will get the final energy as shown below. The computational energy of dissociated F₂ is -198.74386524 hartree.

Total Energy:    -198.74386524

First Excited:   -197.850852

Both coefficients and weights of VB structures show that the wave function includes only covalent structure, indicating that the molecule is dissociated to 2 F\(\cdot\) radicals.

       ******  COEFFICIENTS OF STRUCTURES ******

1     1.00000  ******  1:8    9  10
2     0.00000  ******  1:8    9   9
3     0.00000  ******  1:8   10  10
                      .
                      .
                      .
       ******  WEIGHTS OF STRUCTURES ******

1     1.00000  ******  1:8    9  10
2     0.00000  ******  1:8    9   9
3     0.00000  ******  1:8   10  10

By substracting energies at stationary point and dissociation limit, the BDE can be obtained as 4.4 kcal/mol.

3.4. Computations with Covalent Structure at Stationary Point

3.4.1. Input File

The input file can be obtained by replacing STR=FULL with STR=COV in the input file of 3 structures at stationary point, as shown below.

$CTRL
STR=COV NAO=2 NAE=2 IPRINT=3
ORBTYP=HAO FRGTYP=SAO
BASIS=CC-PVDZ
$END

3.4.2. Computational Results

The structure information is shown below. It can be seen that only 1 covalent structure is generated for this computation.

Number of   0th ion  structures  is:          1  from          1 to          1
Number of   0th ion determinants is:          2  from          1 to          2
Total number of  structures  is:          1
Total number of determinants is:          2
                       .
                       .
                       .
 Number of Structures:           1

 The following structures are used in calculation:

       1 *****  1:8    9  10

The final energy after SCF iteration is -198.67485969 hartree.

Total Energy:    -198.67485969

The Last Change in Energy:  -0.000000

The bond order result in atomic population analysis shows that the bond order with only covalent structure is 0.324, which is much smaller than computations with 3 structures.

          ******  BOND ORDER  ******

ATOM 1        ATOM 2           DIST     BOND ORDER

 1 F           2 F            1.400       0.324

The RE value, 47.6 kcal/mol, can be obtained from energies by covalent and 3 structure computations at stationary point. Compared with the computational BDE 4.4, RE is much larger than BDE, indicating that the chemical bonding in F₂ is an charge-shifting bond. The much smaller bond order data with only covalent structure also indicates that resonance plays an important role in the F-F bonding.