1. Slides for Basic VB Exercises
Slides for basic exercises can be downloaded here.
2. The Understanding of H2
2.1. Introduction
As a multiconfigurational quantum chemical method, a VBSCF calculation starts with the definition of the configuration space, i.e. active space (m,n), in which m active electrons arbitrarily distribute on n active orbitals. One can write totally three VB structures for hydrogen molecule by considering all singlet spin coupling patterns in the (2,2) active space. The three VB structures, namely covalent structure \(\Phi^{cov}\), and two ionic structures \(\Phi_1^{ion}\)and \(\Phi_2^{ion}\), are written as
where \(\phi_a\) and \(\phi_b\) are respectively the atomic orbitals of hydrogens a and b, \(s_{ab}\) is the orbital overlap between \(\phi_a\) and \(\phi_b\), and the bar over an orbital means a β spin orbital. Since no covalent bond is formed in the two ionic structures, each of the ionic structure is described by \(2^0=1\) determinant. The covalent structure consists one covalent bond, and hence is comprised of \(2^1=2\) determinants, namely \(|\phi_a\overline{\phi}_b|\) and \(|\overline{\phi}_a\phi_b|\). Note that neither of the determinants \(|\phi_a\overline{\phi}_b|\) nor \(|\overline{\phi}_a\phi_b|\) is the eigenfunction of \(\hat{S}^2\), and thus should be combined to form a spin-adapted VB structure. The three VB structures and their four expanded determinants are illustrated in the following figure.
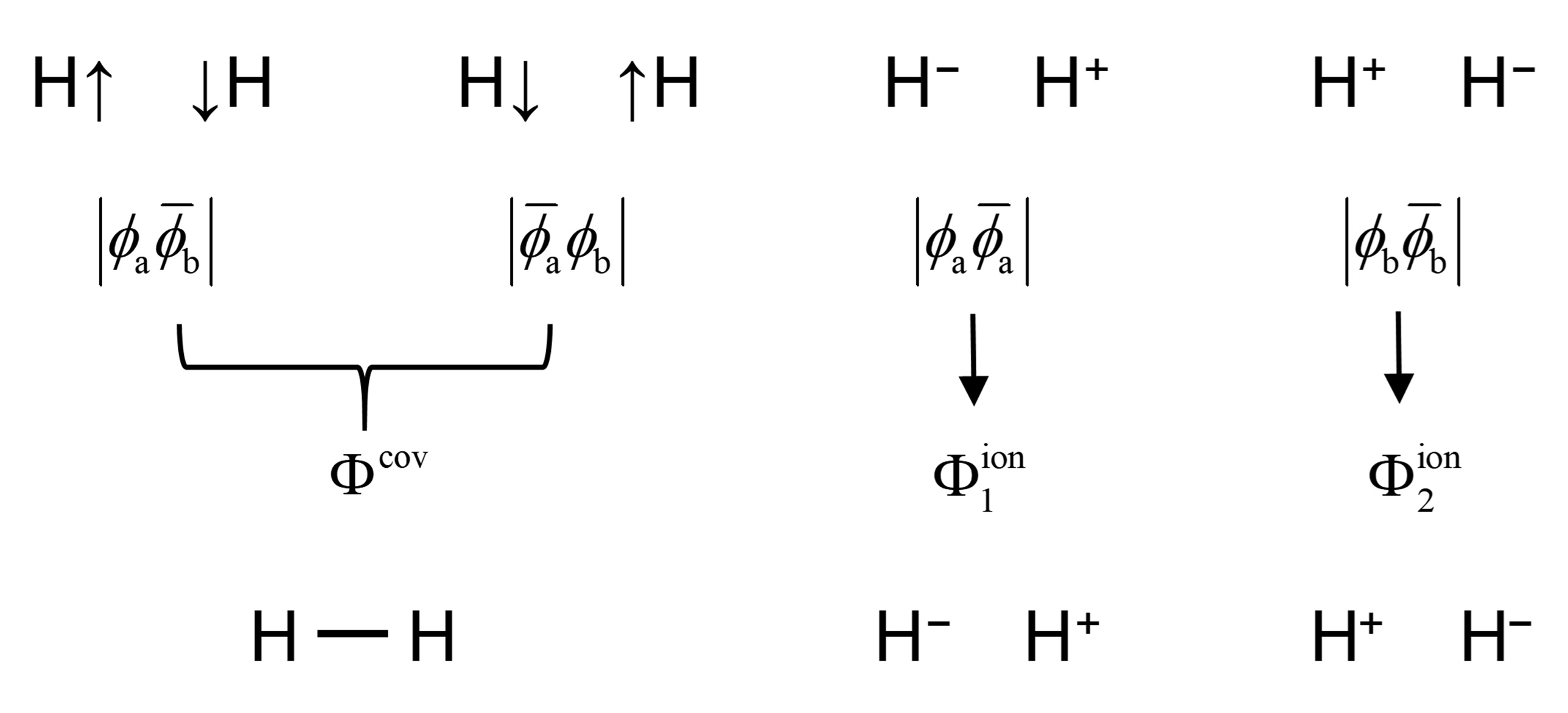
The three VB structures and their four expanded determinants of H2 The VBSCF wave function of H2 molecule can thus be written as
where the coefficients of the two ionic structures are the same according to the symmetry of the H2 molecule. With cc-pvTZ basis set, the Coulson-Chirgwin weights of the three VB structures \(\Phi^{cov}\), \(\Phi_1^{ion}\) and \(\Phi_2^{ion}\) at the equilibrium bond length (R=0.75 Å) are respectively 0.82, 0.09 and 0.09, which indicates that the covalent bonding dominants the H2 molecule, but the ionic character still play a nonnegligible role for the homopolar bond. As the H-H bond stretched, the weight of the covalent structure gradually increases while the weights of the ionic structures decrease. At the dissociation limit the H-H bonding is purely covalent, which corresponds to the two neutral hydrogen atoms after bond dissociation. The following figure plots the weights of the covalent and ionic structures along the dissociation of H2 molecule. We demonstrate again the VB theory is natural multi-determinantal, even when only one covalent structure is involved in the wave function for bond breaking. The multi-determinant feature enables VB theory to correctly treat bond breaking and strongly-correlated systems.
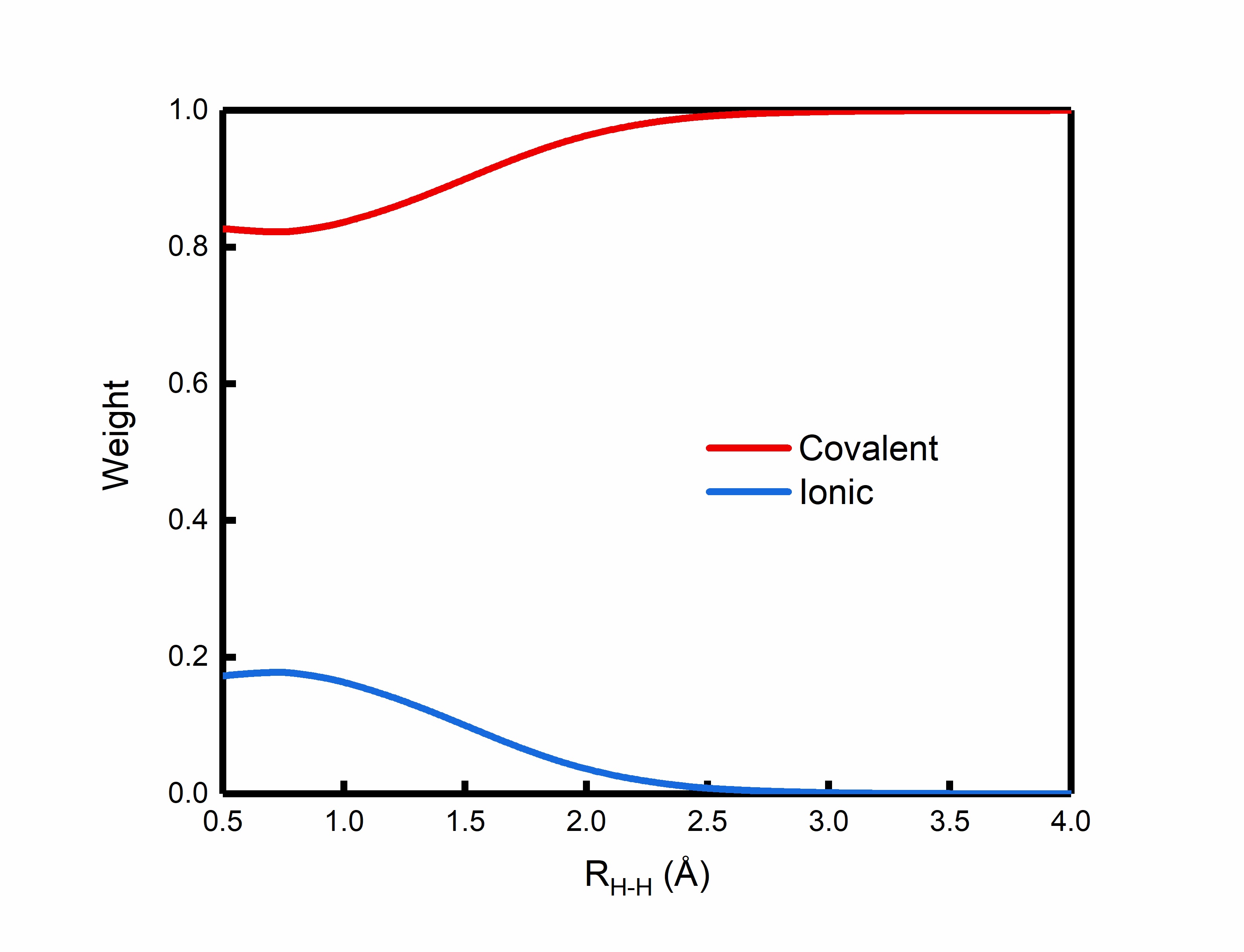
2.2. Computation of H2 at Stationary Point
This exercise will provide a first glance at VB computation. The users will learn the struct and syntax of XMVB input, how to build a simple input file, how to run the job and what we will get from the output.
The computation is proceeded at the equilibrium bond lenght of 0.75 Å, and the basis set is cc-pVDZ. For simplicity, H atoms are located in the Z axis.
2.2.1. Input File
Running an XMVB job requires an input file with extension name “xmi”, which is composed of several sections. The following is an simplest example xmi input file of VBSCF calculation of H2.
H2 VBSCF with 3 structures
$CTRL
STR=FULL NAO=2 NAE=2 IPRINT=3
BASIS=CC-PVDZ
$END
$ORB
5 5
1-5
6-10
$END
$GEO
H 0.0 0.0 0.0
H 0.0 0.0 0.75
$END
The keywords in XMVB are case insensitive. The first line is the title of the job, and followed by several sections starting with $CTRL (or $STR, $ORB, $GEO, etc.) and ending with $END. The order of the sections can be arbitrary. The keywords within each section are separated by blanks and are not limited to a single line.
In an xmi file, the $CTRL and $GEO sections, which correspond to global control and molecular geometry, must be provided by the user, and other sections might be default in some cases.
In the $CTRL section, NAE and NAO are respectively the numbers of active electrons and active orbitals, and (2,2) active space is used in this case;
STR=FULL means all the 3 VB structures in the (2,2) active space are included; BASIS=CC-PVDZ means the cc-pVDZ basis set is used.
No VB method is specified in this inputfile, and the default VBSCF calculation will be performed.
The $ORB section defines the VB orbitals. The first line specifies the numbers of basis functions to expand each orbital, each number separated by blanks.
In this case (“NAO=2”), 5 5 means the two orbitals are expanded with 5 and 5 basis functions. With cc-pVDZ basis set, the basis functions of the first H atom (shown in the first line in $GEO section) are labeled as 1-5,
while those of the second H atom (the second line in $GEO section) are labeled as 6-10. Thus, the second line 1-5 in $orb section means the first orbital is expanded by the basis functions of the first H atom,
while the third line 6-10 means the second orbital is expanded by the basis functions of the second H atom.
2.2.2. Output File
The main XMVB output file has an “xmo” extension. The output file starts with the XMVB banner, then followed by the description of VB structures used in calculation, nuclear repulsion energy, initial orbital guess, and a repetition of the input file. For a VBSCF calculation, the information of orbital optimization (the energy and gradients) at each iteration is printed. After the end of the SCF procedure, the VBSCF wave function is printed, including the Hamiltonian and overlap matrices, VB structure and determinant coefficients, weights of VB structures, and the optimized orbitals. Finally, the charge and spin population analysis, bond order and dipole moments are printed. Following is a detailed explain of H 2 (corresponding to the input file in the previous section).
In the (2,2) active space, totally 3 structures (4 determinents) are involved in the VBSCF wave function.
Number of 0th ion structures is: 1 from 1 to 1
Number of 0th ion determinants is: 2 from 1 to 2
Number of 1th ion structures is: 2 from 2 to 3
Number of 1th ion determinants is: 2 from 3 to 4
Total number of structures is: 3
Total number of determinants is: 4
.
.
.
Number of Structures: 3
The following structures are used in calculation:
1 ***** 1 2
2 ***** 1 1
3 ***** 2 2
The user may find from the output file that the VBSCF converged after 6 iterations and the final energy is -1.14694448 hartree.
VBSCF converged in 6 iterations
Total Energy: -1.14694448
First Excited: -0.268326
The coefficients and weights shows the importance of each structure. Following are the coefficients and weights of generated VB structures. Both coefficients and weights show that the covalent structure is the dominant one. So the H-H bond should be a covalent bond.
****** COEFFICIENTS OF STRUCTURES ******
1 -0.83526891 ****** 1 2
2 -0.09985465 ****** 1 1
3 -0.09985465 ****** 2 2
.
.
.
****** WEIGHTS OF STRUCTURES ******
1 0.83388006 ****** 1 2
2 0.08305997 ****** 1 1
3 0.08305997 ****** 2 2
Finally, the bond order value (0.950) in atomic population analysis shows that H-H bond should be a single bond.
****** BOND ORDER ****** ATOM 1 ATOM 2 DIST BOND ORDER 1 H 2 H 0.750 0.950