8. Computing of diabatic states with VB theory
8.1. Introduction
Molecular dynamical process involving excited states is usually simulated under the Born-Oppenheimer adiabatic approximation, in which the adiabatic electronic states are used to construct the potential energy surfaces (PESs). Adiabatic states are eigenstates of electronic Hamiltonian, and thus unique for a given quantum chemical method. For instance, the eigenstates obtained by solving the generalized secular equation \(\textbf{HC}=\textbf{MCE}\) in VBSCF are adiabatic states. In nonadiabatic dynamics, to solve the quantum equation of motion requires the evaluation of nuclear-momentum couplings (NMCs) \(\textbf{F}_{KL}\)
where \(\Psi_K(\textbf{r};\textbf{R})\) is the electronic wave function of state K with parametrical dependence on the nuclear coordinates \(\textbf{R}\). Specially, \(\textbf{F}_{KL}\) in adiabatic state basis is called nonadiabatic couplings (NACs). The complexity arises near the conical intersections where the NACs have singularities due to the rapid change of the character of the adiabatic wave function. The sudden change of the adiabatic wave function can be understood according to the following figure, which could be interpreted as a conical intersection between one covalent state and one ionic state. Suppose that the adiabatic state \(\Psi_1\) is mainly covalent and \(\Psi_2\) is mainly ionic before the avoided crossing point (\(R^c\)). Then singularity of \(\textbf{F}_{12}\) occurs at \(R^c\) when \(\Psi_1\) rapidly changes to ionic and \(\Psi_2\) rapidly changes to covalent. It is possible to remove such singularity by constructing the PESs with diabatic states. In diabatic state basis, the electronic Hamiltonian is not diagonal, and the effect of the NMCs should be negligible compared with the off-diagonal elements of the electronic Hamiltonian. Therefore, the definition of diabatic states is not unique.
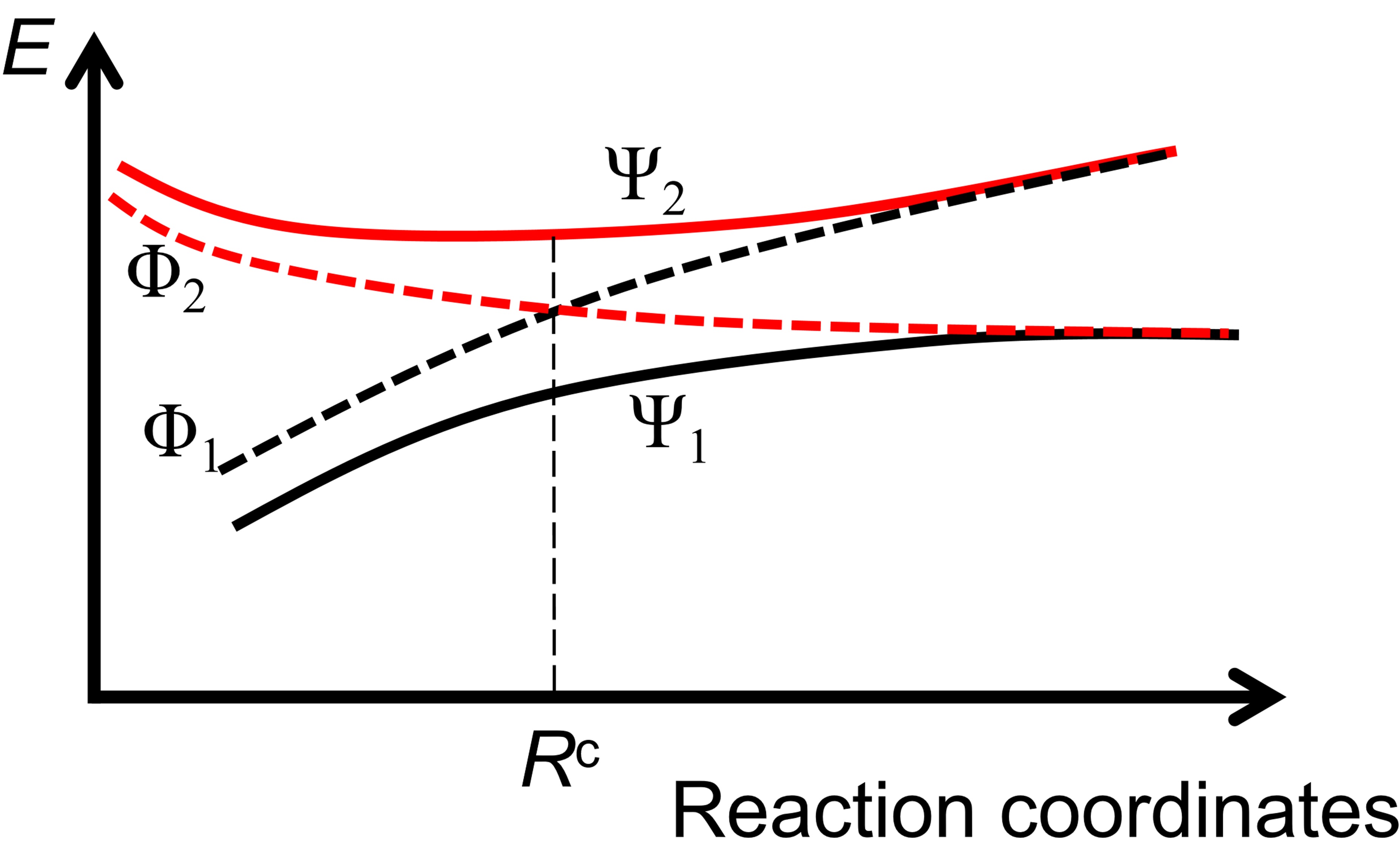
Illustration of adiabatic states (solid lines) and diabatic states (dashed lines).
Various schemes based on molecular orbital theory have been proposed to construct the diabatic states. On the contrary, the construction of diabatic states with VB theory seems more straightforward, since each VB structure exactly corresponds to a Lewis structure, and thus never changes its character along the PES. In this section, two ways to construct diabtic states with VB theory are presented for LiF molecule.
LiF is a simple hetero diatomic molecule with a single bond between atoms Li and F. The dissociation of LiF is always in the interest of chemists. The so-called “Harpoon effect” makes electron transfer when the distance between Li and F even larger than the sum of their van der Waals radius, indicating an electron transfer due to the crossing of diabatic states. For details, please refer to the reference.
In this exercise, users will compute a series of points along the dissociation of LiF for the first two electronic states, get the energies of both the adiabatic and diabatic states with VB theory, and plot the potential energy surface. The basis set in this exercise is cc-pVDZ, and the active space is the minimal (2,2) space, which includes the \(2s\) orbital of Li atom and \(2p_z\) orbital of F atom.
8.2. Computations of adiabatic states
The distance RLi-F is 1.5 Å in the example input file below.
8.2.1. Input file
The first two adiabatic states of LiF
$CTRL
STR=FULL NAO=2 NAE=2 IPRINT=3
ORBTYP=HAO FRGTYP=SAO
BASIS=CC-PVDZ
WSTATE(1)=0.5,0.5 GUESS=READ
$END
$FRAG
1*4
SPZDXXDYYDZZ 1
SPZDXXDYYDZZ 2
PXDXZ 2
PYDYZ 2
$END
$ORB
1*7
1
2
2
3
4
1
2
$END
$GEO
Li 0.0 0.0 0.0
F 0.0 0.0 1.5
$END
$VEC
8 8 8 3 3 8 8
# ORBITAL 1 NAO = 8
1.0006124741 1 0.0010947827 2 -0.0001697524 3 -0.0054823903 6
0.0022720913 9 -0.0024855501 10 -0.0024855494 11 -0.0029391815 12
# ORBITAL 2 NAO = 8
-0.9878720649 16 0.0820885570 17 0.1032423966 18 -0.0041896343 21
-0.0056696719 24 0.0001113470 25 0.0001115264 26 0.0012300179 27
# ORBITAL 3 NAO = 8
0.1608417532 16 0.4836528017 17 0.5898820135 18 -0.0253431901 21
-0.0323439728 24 -0.0057810288 25 -0.0057799058 26 -0.0006485649 27
# ORBITAL 4 NAO = 3
-0.6610782115 19 -0.4931501640 22 0.0078682530 29
# ORBITAL 5 NAO = 3
-0.6610781961 20 -0.4931501514 23 0.0078713335 30
# ORBITAL 6 NAO = 8
-0.0485005246 1 0.3835061386 2 0.5812431299 3 -0.3104635019 6
-0.0450765604 9 0.0269723639 10 0.0269723820 11 -0.0250362698 12
# ORBITAL 7 NAO = 8
-0.0016023849 16 -0.0212026440 17 0.0287929283 18 -0.6406201457 21
-0.5152310378 24 -0.0077601696 25 -0.0077603299 26 0.0077058038 27
$END
Note
There is only a single bond in the molecule, so the minimal active space should be (2,2).
VB structures can be automatically generated as we have seen in the example of F2.
Use keywords
ORBTYP=HAOandFRGTYP=SAOwith proper definition of fragmenets in$FRAGto build the orbitals.The active orbitals should always be placed at the last in
$ORBsection.Orbitals obtained in previous computation can be used as initial guess.
The keyword “WSTATE(1)=0.5,0.5” in the $CTRL section is specified for the state-averaged VBSCF calulation. The state-averaged scheme is needed for the calculation of excited states in multiconfigurational methods. In state-averaged scheme, the wave function for each electronic state is optimized variationally to minimize the averaged energy (E) of interested N states as
where \(E_i\) is the energy of state i, and \(w_i\) is the corresponding weight in the averaged scheme. In most cases, the electronc states are averaged with same weights. In the “WSTATE(K)= \(w_1,w_2,...\)" keyword, the averaged scheme is described as following: the Kth state is averaged with weight w1, the \((K+1)\)th state is averaged with weight w2, and so on. In this case, the first two electronic states are averaged, and the weight of the first state (ground state) is 0.5, and the weight of the second state (first excited state) is also 0.5.
The “GUESS=READ” keyword means the orbital guess is taken from the $VEC section. For a calculation of potential energy curve, the orbital guess is often chosen as the optimal orbitals of the molecuar geometry nearby. The optimal orbitals can be found in the file with “.orb” extension after a calculation is done.
8.2.2. Computation of diabatic states with chemical insights
For LiF molecule, the definition of the first two diabatic states is straightforward, i.e. the covalent structure Li-F and the ionic structure Li+ F-. The input files for the calculations of the two diabatic states are shown below.
The covalent diabatic state of LiF
$CTRL
NSTR=1 NAO=2 NAE=2 IPRINT=3
ORBTYP=HAO FRGTYP=SAO GUESS=READ
BASIS=CC-PVDZ
$END
$FRAG
1*4
SPZDXXDYYDZZ 1
SPZDXXDYYDZZ 2
PXDXZ 2
PYDYZ 2
$END
$ORB
1*7
1
2
2
3
4
1
2
$END
$STR
1:5 6 7
$END
$GEO
Li 0.0 0.0 0.0
F 0.0 0.0 1.5
$END
$VEC
8 8 8 3 3 8 8
# ORBITAL 1 NAO = 8
-1.0011678861 1 -0.0022121270 2 0.0023212935 3 -0.0025335037 6
0.0016875131 9 0.0025270489 10 0.0023274646 13 0.0026480262 15
# ORBITAL 2 NAO = 8
-1.0008168299 16 0.0036845277 17 0.0071487300 18 -0.0001661450 21
-0.0003147690 24 0.0010390175 25 0.0010419561 28 0.0015319075 30
# ORBITAL 3 NAO = 8
-0.0101097268 16 -0.5128227302 17 -0.5703498101 18 0.0266052512 21
0.0288144250 24 0.0021878838 25 0.0021691970 28 -0.0016764977 30
# ORBITAL 4 NAO = 3
0.6907944105 19 0.4597105881 22 -0.0059097276 27
# ORBITAL 5 NAO = 3
0.6907940010 20 0.4597105227 23 -0.0059816036 29
# ORBITAL 6 NAO = 8
-0.0238842027 1 -0.4984202033 2 -0.5284694265 3 0.2687769028 6
0.1065714103 9 -0.0107075041 10 -0.0107111179 13 0.0798765082 15
# ORBITAL 7 NAO = 8
0.0080197261 16 -0.0318421895 17 -0.0744506221 18 0.7073285005 21
0.4345585123 24 0.0040544825 25 0.0040620001 28 -0.0046080448 30
$END
The ionic diabatic state of LiF
$CTRL
NSTR=1 NAO=2 NAE=2 IPRINT=3
ORBTYP=HAO FRGTYP=SAO GUESS=READ
BASIS=CC-PVDZ
$END
$FRAG
1*4
SPZDXXDYYDZZ 1
SPZDXXDYYDZZ 2
PXDXZ 2
PYDYZ 2
$END
$ORB
1*7
1
2
2
3
4
1
2
$END
$STR
1:5 7 7
$END
$GEO
Li 0.0 0.0 0.0
F 0.0 0.0 1.5
$END
$VEC
8 8 8 3 3 8 8
# ORBITAL 1 NAO = 8
-1.0004203054 1 0.0002038534 2 0.0005481657 3 0.0132303641 6
-0.0065003814 9 0.0021658077 10 0.0021658077 13 0.0027685384 15
# ORBITAL 2 NAO = 8
-1.0008305986 16 -0.0017058286 17 0.0010077161 18 0.0003735826 21
-0.0001046315 24 0.0011858422 25 0.0011849757 28 0.0011520210 30
# ORBITAL 3 NAO = 8
0.0205934347 16 -0.4655906963 17 -0.6286682097 18 0.0355102258 21
0.0460224079 24 0.0093958692 25 0.0093958715 28 0.0024192082 30
# ORBITAL 4 NAO = 3
0.6265556203 19 0.5304582609 22 -0.0098651162 27
# ORBITAL 5 NAO = 3
0.6265556195 20 0.5304582617 23 -0.0098651162 29
# ORBITAL 6 NAO = 8
-0.1494486185 1 -0.7392177847 2 0.2171735656 3 -0.7734875826 6
0.2332816045 9 0.3272572338 10 0.3272572338 13 -0.5469570507 15
# ORBITAL 7 NAO = 8
0.0096938330 16 0.0583635389 17 0.0122710208 18 0.6211959886 21
0.5329337539 24 0.0088600826 25 0.0088600766 28 -0.0093045652 30
$END
For the covalent diabatic state Li-F, the corrsponding structure is “1:5 6 7”; For the ionic diabatic state Li+ F-, the corrsponding structure is “1:5 7 7”. From the output files, readers can find the energy of the covalent structure is -106.74408537 hartree, and the energy of the ionic structure is -106.89954237 hartree. Therefore, the bonding of Li-F is dominated by the ionic structure near equilibrium geometry. After bond dissociation, however, the bonding of Li-F is dominated by the covalent structure. The potential energy curves of these two diabatic states are plotted in the following figure.

The potential energy curves of two diabatic states obtained by chmical insights.
Note
Careful readers may notice the potential energy curves of VBSCF adiabatic states are not consistent with those in reference. This is because VBSCF is not accurate enough, and better curves can be obtained with post-VBSCF methods.
8.2.3. Computation of diabatic states with VBCAD
Instead of diabatization scheme with chemical insights, the valence-bond-based compression approach for diabatization (VBCAD), however, is a black-box-like diabatization scheme. In VBCAD, the electronic Hamiltonian is first compressed into a low dimensional matrix Hpre-dia containing only the interested electronic states, and then the diabatic Hamiltonian (Hdia) is obtained by a transformation to Hpre-dia. The transformation is determined by maximizing the separation of VB structures in different electronic states. For more details, please refer to reference.
An example input file for VBCAD calculation is shown below
The first two diabatic states of LiF with VBCAD
$CTRL
STR=FULL NAO=2 NAE=2 IPRINT=3
ORBTYP=HAO FRGTYP=SAO
BASIS=CC-PVDZ
WSTATE(1)=0.5,0.5 GUESS=READ VBCAD
$END
$FRAG
1*4
SPZDXXDYYDZZ 1
SPZDXXDYYDZZ 2
PXDXZ 2
PYDYZ 2
$END
$ORB
1*7
1
2
2
3
4
1
2
$END
$GEO
Li 0.0 0.0 0.0
F 0.0 0.0 1.5
$END
$VEC
8 8 8 3 3 8 8
# ORBITAL 1 NAO = 8
1.0006124741 1 0.0010947827 2 -0.0001697524 3 -0.0054823903 6
0.0022720913 9 -0.0024855501 10 -0.0024855494 11 -0.0029391815 12
# ORBITAL 2 NAO = 8
-0.9878720649 16 0.0820885570 17 0.1032423966 18 -0.0041896343 21
-0.0056696719 24 0.0001113470 25 0.0001115264 26 0.0012300179 27
# ORBITAL 3 NAO = 8
0.1608417532 16 0.4836528017 17 0.5898820135 18 -0.0253431901 21
-0.0323439728 24 -0.0057810288 25 -0.0057799058 26 -0.0006485649 27
# ORBITAL 4 NAO = 3
-0.6610782115 19 -0.4931501640 22 0.0078682530 29
# ORBITAL 5 NAO = 3
-0.6610781961 20 -0.4931501514 23 0.0078713335 30
# ORBITAL 6 NAO = 8
-0.0485005246 1 0.3835061386 2 0.5812431299 3 -0.3104635019 6
-0.0450765604 9 0.0269723639 10 0.0269723820 11 -0.0250362698 12
# ORBITAL 7 NAO = 8
-0.0016023849 16 -0.0212026440 17 0.0287929283 18 -0.6406201457 21
-0.5152310378 24 -0.0077601696 25 -0.0077603299 26 0.0077058038 27
$END
The keyword “VBCAD” is specified for a black-box-like diabatization with VB theory. Currently, VBCAD supports diabatization with only 2 electronic states.
In the output file, the Hamiltonian in the diabatic state basis is printed out as
****** Diabatic Hamiltonian ******
1 2
1 -106.714613 0.013448
2 0.013448 -106.877770
followed by the printing of energy and wave function of each diabatic state.
VBCAD DIABATIC STATE: 1
VBCAD DIABATIC ENERGY: -106.714613
****** COEFFICIENTS OF STRUCTURES ******
1 1.00169 ****** 1:5 6 7
2 -0.01716 ****** 1:5 6 6
3 -0.02505 ****** 1:5 7 7
CC Weights
1 1.00123 ****** 1:5 6 7
2 -0.00058 ****** 1:5 6 6
3 -0.00065 ****** 1:5 7 7
.
.
.
VBCAD DIABATIC STATE: 2
VBCAD DIABATIC ENERGY: -106.877770
****** COEFFICIENTS OF STRUCTURES ******
1 0.02599 ****** 1:5 6 7
2 0.00044 ****** 1:5 6 6
3 -1.00099 ****** 1:5 7 7
CC Weights
1 -0.00065 ****** 1:5 6 7
2 0.00000 ****** 1:5 6 6
3 1.00065 ****** 1:5 7 7
It can be found from the CC weights section, the covalent structure Li-F dominats the ground diabatic state, while the ionic structure Li+ F- dominats the first excited diabatic state. This is in consistent with the fact that near equilibrium Li-F bond length, the ground diabatic state is described as covalent, and the first excited diabatic state is described as ionic.
The potential energy curves of these two VBCAD states together with the adiabatic states are plotted in the following figure.
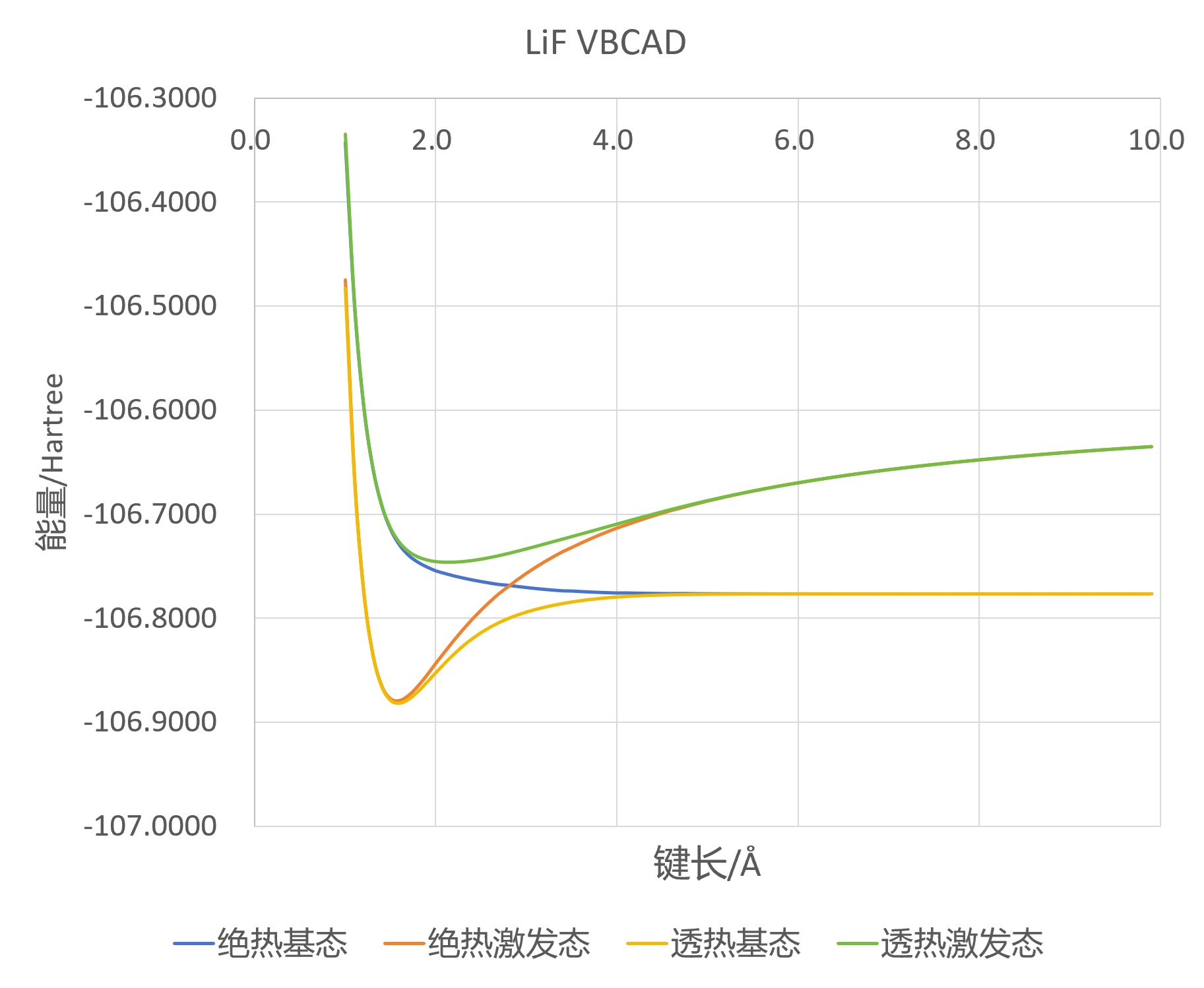
The potential energy curves of the VBCAD states together with the adiabatic states.