3. Universal machine learning models
3.1. Slides
3.2. What are the universal ML models?
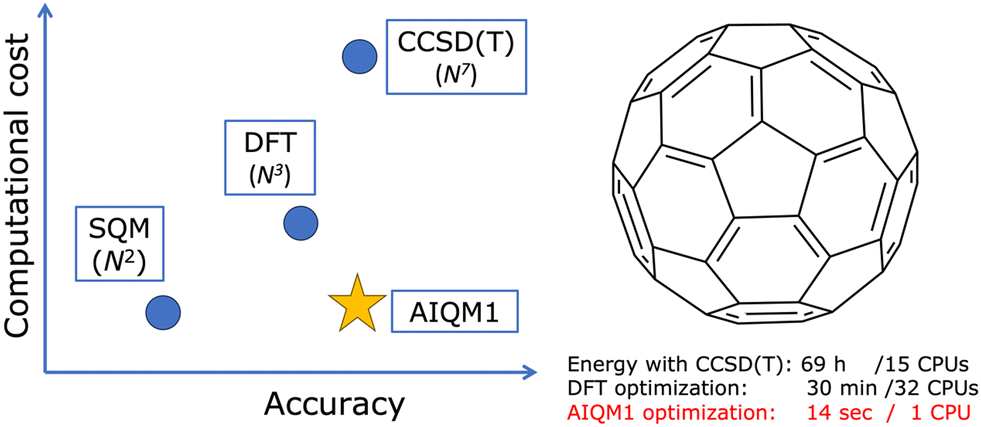
Before we saw that ML models can be very fast and accurate at the same time. However, we needed to use (and train) the model specifically for the H2 example. This is not ideal and it would be nice to have ML models that can be applied to different systems of interest without needing specific training. Such models do exist and they are referred in literature as universal ML models. Example of the universal ML-based model is the UAIQM and its earliest incarnation AIQM1:
[Figure credit: reproduced from Pavlo O. Dral. AI in computational chemistry through the lens of a decade-long journey. Chem. Commun. 2024, 60, 3240–3258. DOI: 10.1039/D4CC00010B under the CC-BY license.]
AIQM1 is approaching the accuracy of CCSD(T)/CBS method and it is an ML-improved semi-empirical QM method, i.e., it is slower than a pure ML model. An example of a pure ML model is ANI-1ccx which also targets the accuracy of the CCSD(T)/CBS method (and, in fact, was published earlier than AIQM1). If both AIQM1 and ANI-1ccx methods are approaching the same CCSD(T)/CBS, then why bother using slower AIQM1? Let’s run an experiment:
Example ML-uni-1.
Optimize geometries of H2 and H2O with ANI-1ccx and AIQM1 (you are welcome to try UAIQM too!).
Check:
Method you used.
Bond lengths (and angle for H2O) you obtained.
How much time it took to complete the calculations.
Example of an input file:
geomopt # Request geometry optimization
AIQM1 # or ANI-1ccx - no model file is needed!
XYZfile='
2
H 0.0000000000000 0.0000000000000 0.0000000000000
H 0.0000000000000 0.0000000000000 0.7000000000000
'
optXYZ=h2_opt_AIQM1.xyz # optimized geometry output (this line is optional, by default it will be in optgeoms.xyz)
After you run these simulations, you should have obtained the following result (compared to other approaches):

One thing that you have noticed is that calculations with both methods are indeed very fast, much faster than with CCSD(T) methods you tried in your homework or task in Lecture 1. The optimized geometry of water molecule is also very close to experimental structure, much closer than with a slower B3LYP/6-31G* method. ANI-1ccx is slightly worse but still provides very good agreement with experiment for H2O.
Note
AIQM1 requires the semi-empirical program. On MLatom@XACS cloud computing service we cannot use MNDO which supports analytical gradients and excited-state simulations but use the development version of SCINE Sparrow (see also a paper on Sparrow). This version does not support analytical gradients and no excited-state calculations with AIQM1. Hence, Sparrow can be used with numerical gradients for geometry optimizations and MD but might lead to numerical instabilities in, e.g., frequency calculations.
There is no such problem with UAIQM.
However, you might be surprised how bad ANI-1ccx is for H2. AIQM1 is also far from CCSD(T) quality. What happened?
AIQM1 and ANI-1ccx are both approaching CCSD(T)/CBS but AIQM1 ≠ ANI-1ccx ≠ CCSD(T)/CBS! They are ML-based models and trained on data which might or might not contain enough training points for H2. How the model was trained is also important. In general, you observe that AIQM1 is more robust than ANI-1ccx for the price of being slower. We will explore why AIQM1 is better in the future lectures.
The important lesson to learn is that any ML model might have limitations (like QM models too). Hence, always pay attention and use your expertise to check the results, i.e., by following recommendations:
compare with other high-level QM calculations (which can be unavailable or prohibitively expensive),
compare to experiment (may be not reliable either!),
check uncertainty (easiest and often works, see the second part or this lecture).
Those were just few molecules we checked. Overall, the quality of AIQM1 is excellent as evidenced by extensive benchmarks on many different molecules which show that AIQM1 optimized geometries are close to experiment and definetely better than many popular DFT methods which might even be qualitatively wrong (see example below for C18 carbon):

[Figure credit: reproduced from Pavlo O. Dral. AI in computational chemistry through the lens of a decade-long journey. Chem. Commun. 2024, 60, 3240–3258. DOI: 10.1039/D4CC00010B under the CC-BY license.]
Even more, AIQM1 was used to revise experimental geometries obtained via X-ray diffraction (see figure above).
You can safely use AIQM1 for quite large systems, where it is faster and more accurate than DFT, i.e., no reason to spend more time with DFT to get worse result!
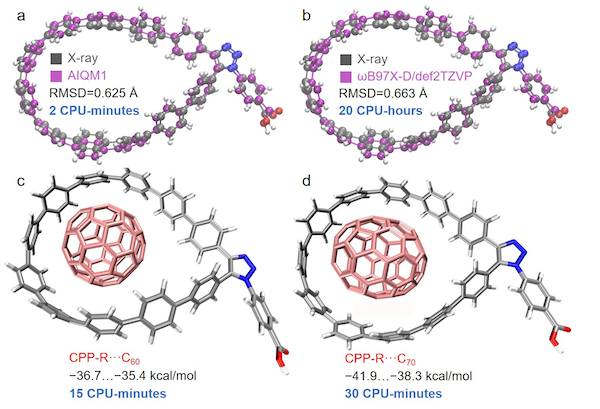
[Figure credit: reproduced from Pavlo O. Dral, et al. MLatom 3: A Platform for Machine Learning-enhanced Computational Chemistry Simulations and Workflows, J. Chem. Theory Comput. 2024, 20, 1193–1213. DOI: 10.1021/acs.jctc.3c01203 under CC-BY 4.0 license.]
You should be, however, aware of the current limitations of the universal models in general. See up-to-date list. The models available in MLatom on July 3, 2024, are overviewed below (partly based on exerpt from the MLatom 3 paper):
Our best offering: the UAIQM models.
Universal potentials ANI-1ccx, ANI-1x, ANI-2x, ANI-1x-D4, ANI-2x-D4, AIMnet-2, ANI-1xnr.
ANI-1ccx is the most accurate and approaches gold-standard CCSD(T) accuracy. Other methods approach the density functional theory (DFT) level.
ANI-1ccx and ANI-1x are limited to CHNO elements, while ANI-2x can be used for CHNOFClS elements.
We allow the user to use D4 dispersion-corrected universal ANI potentials that might be useful for noncovalent complexes.
Hybrid QM/ML methods AIQM1, AIQM1@DFT, AIQM1@DFT*, and DM21 are more transferable and accurate than pretrained ML models but slower (the speed of semiempirical QM methods, which are still much faster than DFT).
AIQM1 is approaching gold-standard CCSD(T) accuracy, while AIQM1@DFT and AIQM1@DFT* target the DFT accuracy for neutral, closed-shell molecules in their ground state. All these methods are limited to the CHNO elements. AIQM1 and AIQM1@DFT include explicit D4 dispersion corrections for the ωB97X functional, while AIQM1@DFT* does not.
These methods can also be used to calculate charged species, radicals, excited states, and other QM properties such as dipole moments, charges, oscillator strengths, and nonadiabatic couplings.
3.3. Frequencies and thermochemistry
After geometry optimization, the next step is to do frequency calculations (typically within rigid-rotor harmonic oscillator approximation) which achieves several goals: 1) obtain zero-point vibrational energy (molecules are always in motion and this should be taken into account!), 2) other thermochemical properties (enthalpies, Gibbs free energies, heats of formation, etc.), 3) perform normal mode analysis to check the nature of vibrations and their frequencies. These calculations also allow you to check whether your optimized geometries correspond to a true minima on potential energy surface (PES) - the minima have all real frequencies while you will see imaginary (shown as negative) frequencies for non-minima.
In principle, AIQM1 and ANI-1ccx are able to deliver very accurate thermochemical properties, particularly heats of formation with close-to chemical accuracy (errors not much larger than 1 kcal/mol). See it for yourself:
Example ML-uni-2.
Calculate frequencies in H2, H2O, and vinylacetylene molecules with ANI-1ccx.
Analyze your calculation results:
Are your optimized geometries true minima?
What are the heats of formation?
Is any of the calculations uncertain?
Example of an input file:
freq # Request frequency and thermochemistry calculations
ANI-1ccx
XYZfile=h2_opt_ani1ccx.xyz # file with optimized geometry
Note
First, you need to optimize geometries as described in the previous tasks. Frequency calculations must be performed at the same level as geometry optimizations.
Initial geometry for vinylacetylene:
8
C 0.00000 0.00000 0.00000
C 1.33718 0.00000 0.00000
C 2.04862 1.23465 0.00000
C 2.65517 2.30065 0.00000
H 3.17326 3.20500 0.00000
H -0.56880 0.91919 0.00000
H -0.56652 -0.92292 -0.00000
H 1.95564 -0.90366 0.00000
Note
Frequency calculations require the evaluation of the second-order energy derivatives. Many methods do not have analytical derivatives, while numerical derivatives are often noisy and may lead to high inaccuracies and lots of negative frequencies which are artificial. This is the case, e.g., if AIQM1 is used on the cloud where the default QM program is Sparrow which has no analytical derivatives for AIQM1. Check in the MLatom program output what program is used - Sparrow (not reliable yet) or MNDO (can be trusted). Calculations with the semiempirical MNDO program are possible but the reader has to install it locally as described in MLatom’s documentation.
Creation of the initial XYZ geometry of vinylacetylene takes time. We do provide you with the initial guess, but what is a faster way to get XYZ geometry for a new molecule? I have asked ChatGPT in 2023 to generate XYZ coordinates or an input file for Gaussian program and it generated some gibberish:
That might improve with time though. One more trick is to look up the coordinates in the internet as many molecules were already either calculated or have known experimental structures. Indeed, for vinylacetylene we can find XYZ structure optimized at a quite decent CCSD(T)/6-31G* level of theory and made available on a very useful NIST website (check it out – it is a treasure trove for any chemist!):
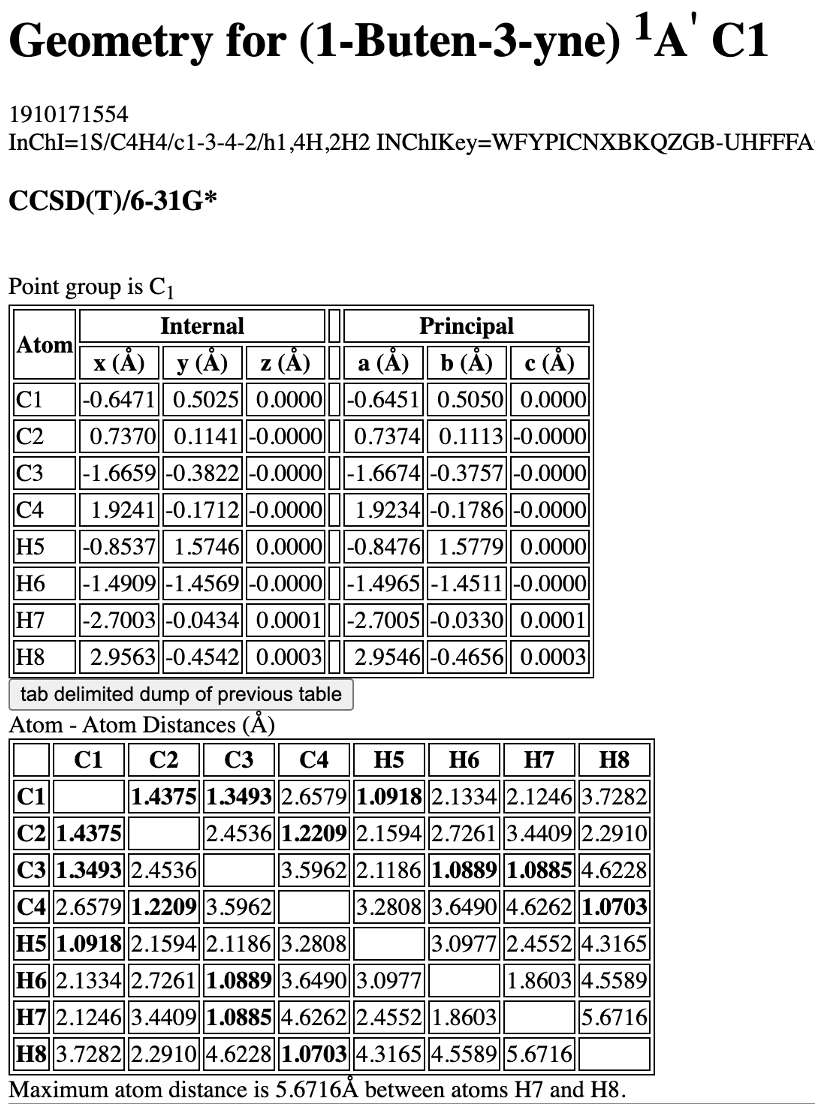
Going back to our exercise, you can find that for water molecule, it has no negative frequencies, i.e., it is a true minimum. Its heat of formation is predicted to be -58.46 kcal/mol at AIQM1 which is quite close to the experimental value of -57.8 kcal/mol (in gas phase! [J.B.Pedley, R.D.Naylor, and S.P.Kirby, “Thermochemical Data of Organic Compounds”, 2nd ed., Chapman and Hall, London, 1986]; the error is only 0.7 kcal/mol). And there is no warning about uncertainty, see below. The output file looks like this:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
Rotational symmetry number: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 1734.1034 1.0833 1.9194
2 3809.1282 1.0819 9.2489
3 3829.5496 1.0449 9.0285
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NNs : 0.00028358 Hartree 0.17795 kcal/mol
Energy : -76.38362520 Hartree
ZPE-exclusive internal energy at 0 K: -76.38363 Hartree
Zero-point vibrational energy : 0.02135 Hartree
Internal energy at 0 K: -76.36227 Hartree
Enthalpy at 298 K: -76.35849 Hartree
Gibbs free energy at 298 K: -76.38056 Hartree
Atomization enthalpy at 0 K: 0.35083 Hartree 220.14828 kcal/mol
ZPE-exclusive atomization energy at 0 K: 0.37218 Hartree 233.54734 kcal/mol
Heat of formation at 298 K: -0.09316 Hartree -58.45749 kcal/mol
==============================================================================
Just for your reference, it is -58.33 kcal/mol at AIQM1 (the error of only 0.5 kcal/mol), see the output file:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 1654.6962 1.0829 1.7470
2 3850.4309 1.0449 9.1277
3 3931.4391 1.0817 9.8508
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NN contribution : 0.00009088 Hartree 0.05703 kcal/mol
NN contribution : -0.00110508 Hartree
Sum of atomic self energies : -63.04934947 Hartree
ODM2* contribution : -13.33326549 Hartree
D4 contribution : -0.00002289 Hartree
Total energy : -76.38374293 Hartree
ZPE-exclusive internal energy at 0 K: -76.38374 Hartree
Zero-point vibrational energy : 0.02150 Hartree
Internal energy at 0 K: -76.36225 Hartree
Enthalpy at 298 K: -76.35847 Hartree
Gibbs free energy at 298 K: -76.37988 Hartree
Atomization enthalpy at 0 K: 0.35062 Hartree 220.01876 kcal/mol
ZPE-exclusive atomization energy at 0 K: 0.37212 Hartree 233.50896 kcal/mol
Heat of formation at 298 K: -0.09295 Hartree -58.32770 kcal/mol
==============================================================================
Wall-clock time: 4.54 s (0.08 min, 0.00 hours)
MLatom terminated on 25.04.2024 at 11:15:15
==============================================================================
3.4. Uncertainty quantification
For hydrogen molecule, we see that it is also a true minimum, its heat of formation is -23.09 kcal/mol. And as a chemist, you must know what the experimental value is and realize that the error is too large. However, you will notice that the output file contains a warning message * Warning * Heat of formation have high uncertainty!:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
Rotational symmetry number: 1
This is a linear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 2866.6581 1.0080 4.8805
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NNs : 0.00705607 Hartree 4.42775 kcal/mol
Energy : -1.20973475 Hartree
ZPE-exclusive internal energy at 0 K: -1.20973 Hartree
Zero-point vibrational energy : 0.00653 Hartree
Internal energy at 0 K: -1.20320 Hartree
Enthalpy at 298 K: -1.19990 Hartree
Gibbs free energy at 298 K: -1.21434 Hartree
Atomization enthalpy at 0 K: 0.20144 Hartree 126.40693 kcal/mol
ZPE-exclusive atomization energy at 0 K: 0.20797 Hartree 130.50502 kcal/mol
Heat of formation at 298 K: -0.03680 Hartree -23.09143 kcal/mol
* Warning * Heat of formation have high uncertainty!
==============================================================================
For your reference, the heat of formation at AIQM1 is not very accurate either: it is -2.86 kcal/mol and uncertain too:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
This is a linear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 3500.7003 1.0078 7.2769
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NN contribution : 0.00891919 Hartree 5.59688 kcal/mol
NN contribution : -0.00210675 Hartree
Sum of atomic self energies : -0.08587317 Hartree
ODM2* contribution : -1.09094346 Hartree
D4 contribution : -0.00000889 Hartree
Total energy : -1.17893227 Hartree
ZPE-exclusive internal energy at 0 K: -1.17893 Hartree
Zero-point vibrational energy : 0.00797 Hartree
Internal energy at 0 K: -1.17096 Hartree
Enthalpy at 298 K: -1.16765 Hartree
Gibbs free energy at 298 K: -1.18240 Hartree
Atomization enthalpy at 0 K: 0.16920 Hartree 106.17224 kcal/mol
ZPE-exclusive atomization energy at 0 K: 0.17717 Hartree 111.17663 kcal/mol
Heat of formation at 298 K: -0.00455 Hartree -2.85652 kcal/mol
* Warning * Heat of formation have high uncertainty!
==============================================================================
Wall-clock time: 4.49 s (0.07 min, 0.00 hours)
MLatom terminated on 25.04.2024 at 11:26:42
==============================================================================
Indeed, the calculations have high uncertainty as judged by the standard deviation of neural network (NN) contribution, it is quite large: 4.43 and 5.60 kcal/mol at ANI-1ccx and AIQM1, respectively, compared to only 0.18 and 0.06 kcal/mol for a water molecule. AIQM1 and ANI-1ccx both contain many (eight) NNs whose predictions are averaged. These NNs learned the same property and, hence, if they start to deviate from each other it means they are likely to stray away too far from the region they were trained on. The deviation between NNs is often used in ML to judge how bad the predictions are (e.g., used in query by committee and active learning, see next lectures). The question is how large deviation is still acceptable and hence we calibrated them on a standard data set and MLatom flags when deviation exceeds the calibrated thresholds.
This is consistent with our previous observation that ANI-1ccx and AIQM1 are not particularly good for the H2 molecule, i.e., the optimized bond lengths were quite off from the experimental value.
In case of vinylacetylene, we observe that it is also true minimum, its heat of formation is 68.53 kcal/mol, and it is not uncertain:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
Rotational symmetry number: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 234.3120 3.5401 0.1145
2 305.3683 2.6251 0.1442
3 542.0444 1.4458 0.2503
4 546.4789 1.2326 0.2169
5 559.3526 2.3867 0.4400
6 588.7133 1.5581 0.3182
7 900.8130 1.3032 0.6230
8 966.6489 2.6463 1.4569
9 991.1206 1.2769 0.7390
10 1163.7123 1.4019 1.1185
11 1332.3004 1.4117 1.4764
12 1499.1878 1.2277 1.6258
13 1750.8294 4.0546 7.3229
14 2206.4408 5.7716 16.5550
15 3205.7596 1.0906 6.6035
16 3262.3771 1.0654 6.6806
17 3342.5988 1.1208 7.3781
18 3388.8071 1.1735 7.9404
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NNs : 0.00057841 Hartree 0.36296 kcal/mol
Energy : -154.53147078 Hartree
ZPE-exclusive internal energy at 0 K: -154.53147 Hartree
Zero-point vibrational energy : 0.06102 Hartree
Internal energy at 0 K: -154.47045 Hartree
Enthalpy at 298 K: -154.46484 Hartree
Gibbs free energy at 298 K: -154.49658 Hartree
Atomization enthalpy at 0 K: 1.29896 Hartree 815.10992 kcal/mol
ZPE-exclusive atomization energy at 0 K: 1.35999 Hartree 853.40367 kcal/mol
Heat of formation at 298 K: 0.10920 Hartree 68.52699 kcal/mol
==============================================================================
At AIQM1, the heat of formation is 69.04 kcal/mol and is also confident:
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 203.2675 3.0894 0.0752
2 293.6230 2.4319 0.1235
3 537.1646 3.5850 0.6095
4 671.2905 1.5015 0.3987
5 686.5656 1.2252 0.3403
6 720.9366 1.4999 0.4593
7 879.5200 2.4730 1.1271
8 931.0665 1.3842 0.7070
9 996.7269 1.0846 0.6348
10 1099.9357 1.6593 1.1828
11 1313.2985 1.3102 1.3315
12 1431.8700 1.2556 1.5167
13 1645.4021 3.8620 6.1603
14 2162.6121 6.3527 17.5052
15 3135.1808 1.0791 6.2496
16 3174.0848 1.0667 6.3318
17 3260.7611 1.1187 7.0083
18 3456.1498 1.1511 8.1013
==============================================================================
Thermochemistry for molecule 1
==============================================================================
Standard deviation of NN contribution : 0.00008761 Hartree 0.05498 kcal/mol
NN contribution : 0.00715111 Hartree
Sum of atomic self energies : -133.90358074 Hartree
ODM2* contribution : -20.63402319 Hartree
D4 contribution : -0.00056531 Hartree
Total energy : -154.53101813 Hartree
ZPE-exclusive internal energy at 0 K: -154.53102 Hartree
Zero-point vibrational energy : 0.06060 Hartree
Internal energy at 0 K: -154.47042 Hartree
Enthalpy at 298 K: -154.46492 Hartree
Gibbs free energy at 298 K: -154.49656 Hartree
Atomization enthalpy at 0 K: 1.29803 Hartree 814.52617 kcal/mol
ZPE-exclusive atomization energy at 0 K: 1.35863 Hartree 852.55199 kcal/mol
Heat of formation at 298 K: 0.11002 Hartree 69.04119 kcal/mol
==============================================================================
Wall-clock time: 6.03 s (0.10 min, 0.00 hours)
MLatom terminated on 25.04.2024 at 11:31:47
==============================================================================
Nevertheless, the experimental value used in one of the databases for fitting semi-empirical methods, was 73 kcal/mol. This value deviates from both ANI-1ccx and AIQM1’s predictions by 4 kcal/mol which is too much for confident calculations. Hence, we double checked (and you can too) by calculating the value with another QM method (G4 as implemented in the Gaussian program) and it also gave heat of formation of 69.1 kcal/mol, i.e., basically the same as AIQM1. Hence, I suspected that something might be wrong with that experimental value and, indeed, I found in the NIST database a value of 70.4 kcal/mol which is much closer to the ANI-1ccx and AIQM1 predictions. This is another example (among many similar) where accurate AIQM1 calculations helped to revise the experimental values.
Now let’s see what we can get if we use DFT.
Example ML-uni-3.
Calculate heat of formation of H2O with B3LYP/6-31G*.
Report:
What is the heat of formation?
Is this calculation uncertain?
Example of an input file (do not forget to optimize geometry too!):
freq # Request frequency and thermochemistry calculations
method=B3LYPG/6-31G* # Using PySCF instead of Gaussian
qmprog=pyscf # Use PySCF instead of Gaussian
freqprog=pyscf
XYZfile=h2o_opt_B3LYP.xyz # file with optimized geometry
As you can see in the output file, the heat of formation at B3LYP is -42.30 kcal/mol which is very wrong compared to the experimental -57.8 kcal/mol!
==============================================================================
Vibration analysis for molecule 1
==============================================================================
Multiplicity: 1
Rotational symmetry number: 1
This is a nonlinear molecule
Mode Frequencies Reduced masses Force Constants
(cm^-1) (AMU) (mDyne/A)
1 1710.8681 1.0830 1.8677
2 3720.9628 1.0452 8.5264
3 3843.9202 1.0813 9.4132
==============================================================================
Thermochemistry for molecule 1
==============================================================================
ZPE-exclusive internal energy at 0 K: -76.36989 Hartree
Zero-point vibrational energy : 0.02113 Hartree
Internal energy at 0 K: -76.34876 Hartree
Enthalpy at 298 K: -76.34498 Hartree
Gibbs free energy at 298 K: -76.36708 Hartree
Atomization enthalpy at 0 K: 0.32508 Hartree 203.98967 kcal/mol
ZPE-exclusive atomization energy at 0 K: 0.34621 Hartree 217.25003 kcal/mol
Heat of formation at 298 K: -0.06741 Hartree -42.29876 kcal/mol
==============================================================================
Wall-clock time: 3.43 s (0.06 min, 0.00 hours)
It is indeed well known that DFT methods struggle with getting heats of formation properly. We will discuss this issue in the next lecture.
Another important observation is that DFT (or any other QM method) never provides you any uncertainty of its prediction! This is a big advantage of ML methods that they do provide uncertainty quantification. That’s why when many people complain that they are not sure whether ML is good, they forget that they can never be sure whether their DFT method is good. In ML we at least get an uncertainty of predictions and can improve the ML model later with more data.
3.5. Qualitative problems with PES shape
One of the problems with ML and universal ML is that they often do not describe correctly the dissociation curves of molecules. See it for yourself:
Example ML-uni-4.
Optimize and calculate frequencies of H2 with ANI-1ccx but starting not from initial bond length of 0.7 A as in the previous task but with 0.8 A.
Questions:
Is the geometry you have obtained the same as in the previous task?
Is your optimized geometry true minimum?
What is its heats of formation?
Is this calculation certain?